1题目

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

示例 1：

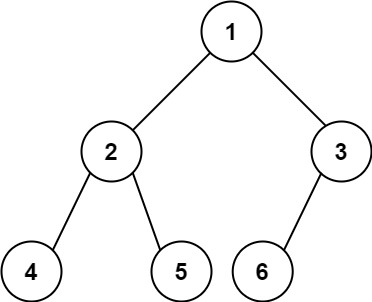
输入：root = [1,2,3,4,5,6]

输出：6

示例 2：

输入：root = []

输出：0

2链接

题目：222. 完全二叉树的节点个数 - 力扣（Leetcode）

视频：要理解普通二叉树和完全二叉树的区别！ | LeetCode：222.完全二叉树节点的数量_哔哩哔哩_bilibili

3解题思路

在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1) 个节点。

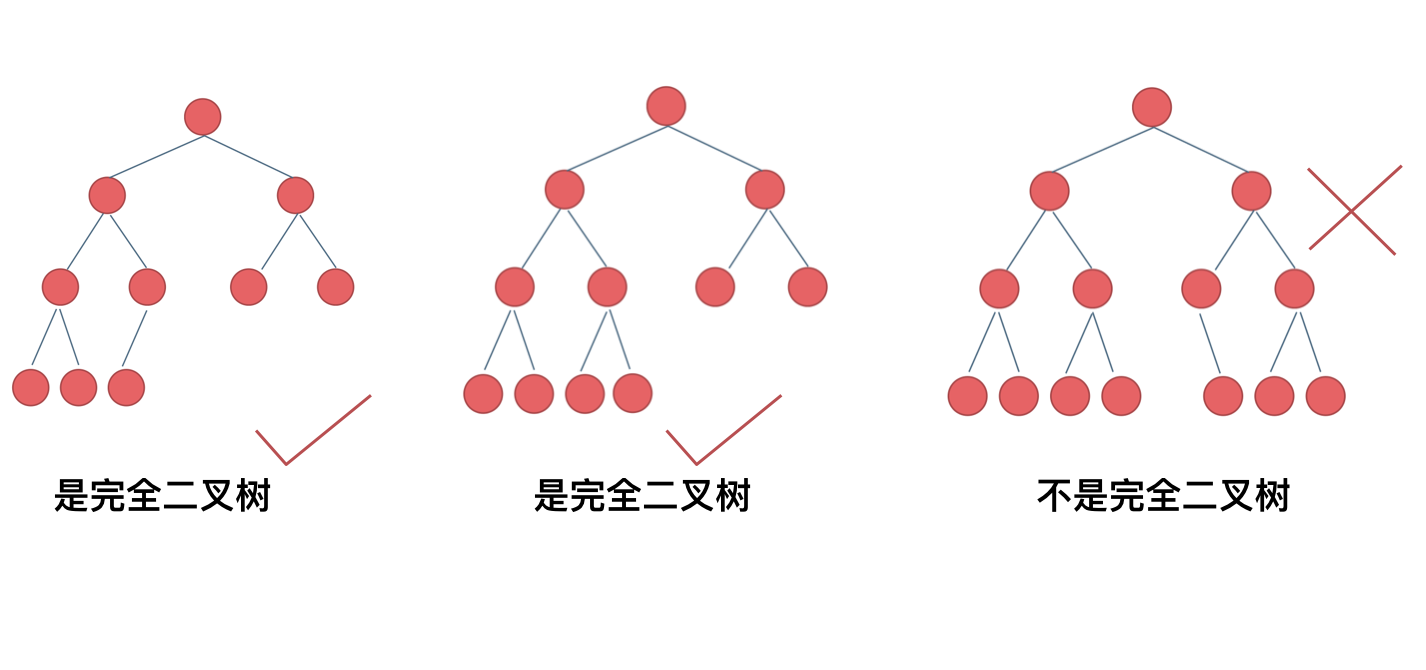
完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。

对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。

对于情况二，分别递归左孩子，和右孩子，递归到某一深度一定会有左孩子或者右孩子为满二叉树，然后依然可以按照情况1来计算。

完全二叉树（一）如图：

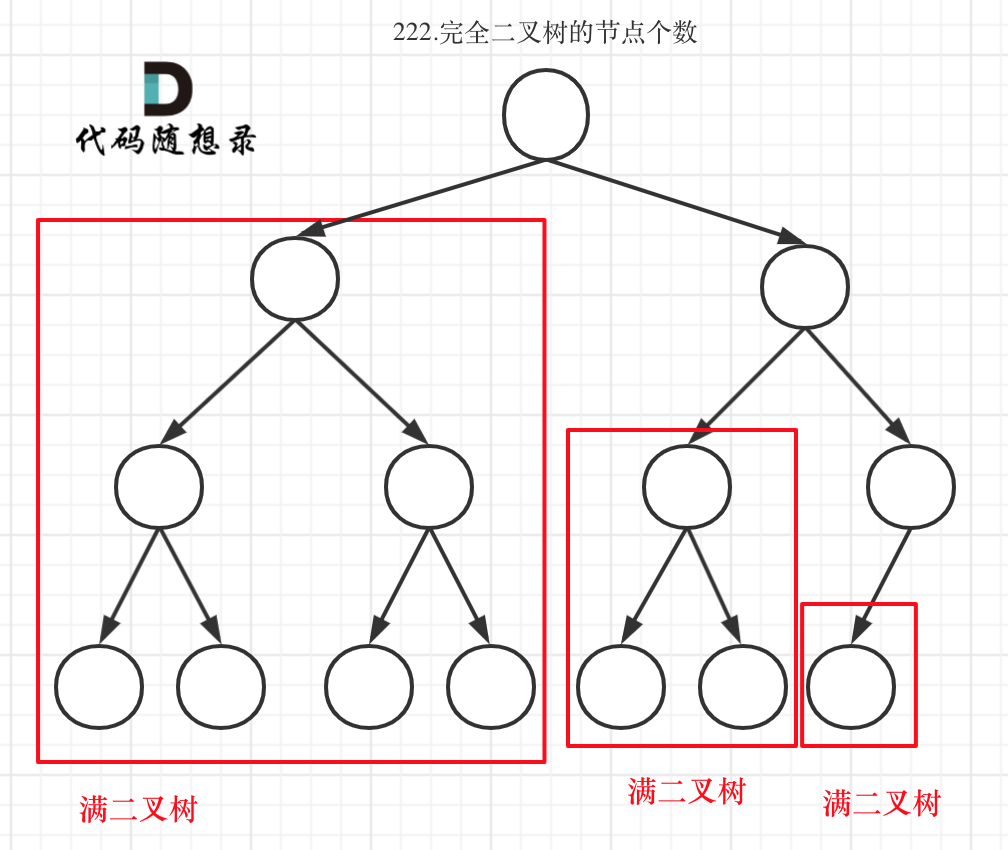
完全二叉树（二）如图：

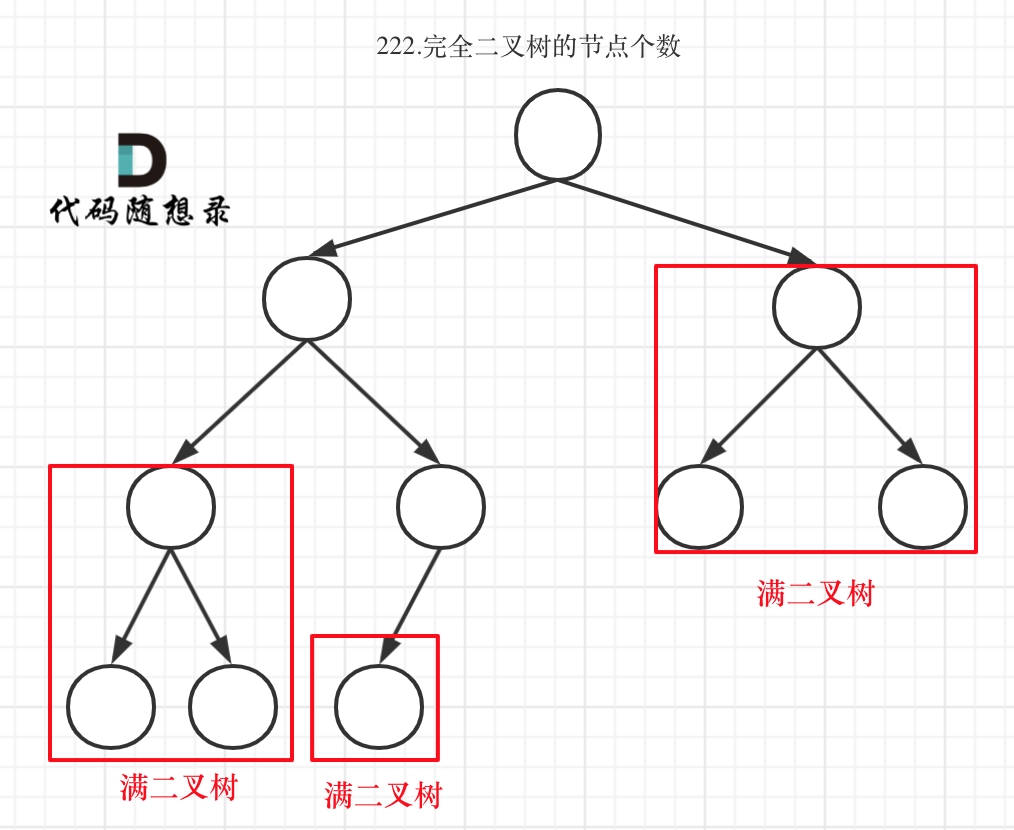
可以看出如果整个树不是满二叉树，就递归其左右孩子，直到遇到满二叉树为止，用公式计算这个子树（满二叉树）的节点数量。

这里关键在于如何去判断一个左子树或者右子树是不是满二叉树呢？

在完全二叉树中，如果递归向左遍历的深度等于递归向右遍历的深度，那说明就是满二叉树。如图：

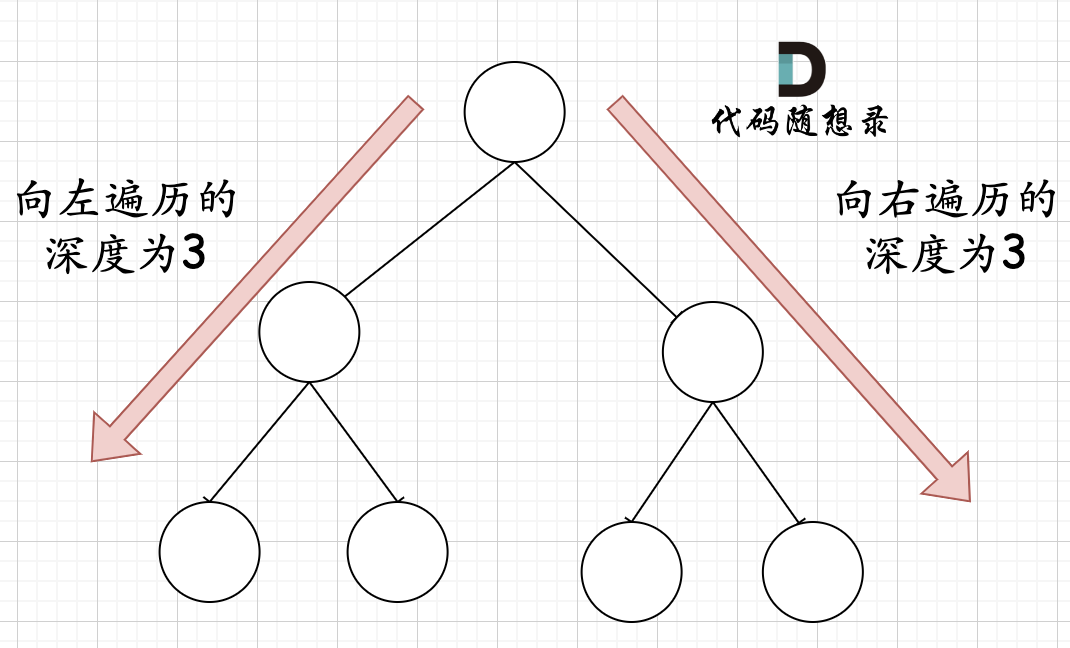
在完全二叉树中，如果递归向左遍历的深度不等于递归向右遍历的深度，则说明不是满二叉树，如图：

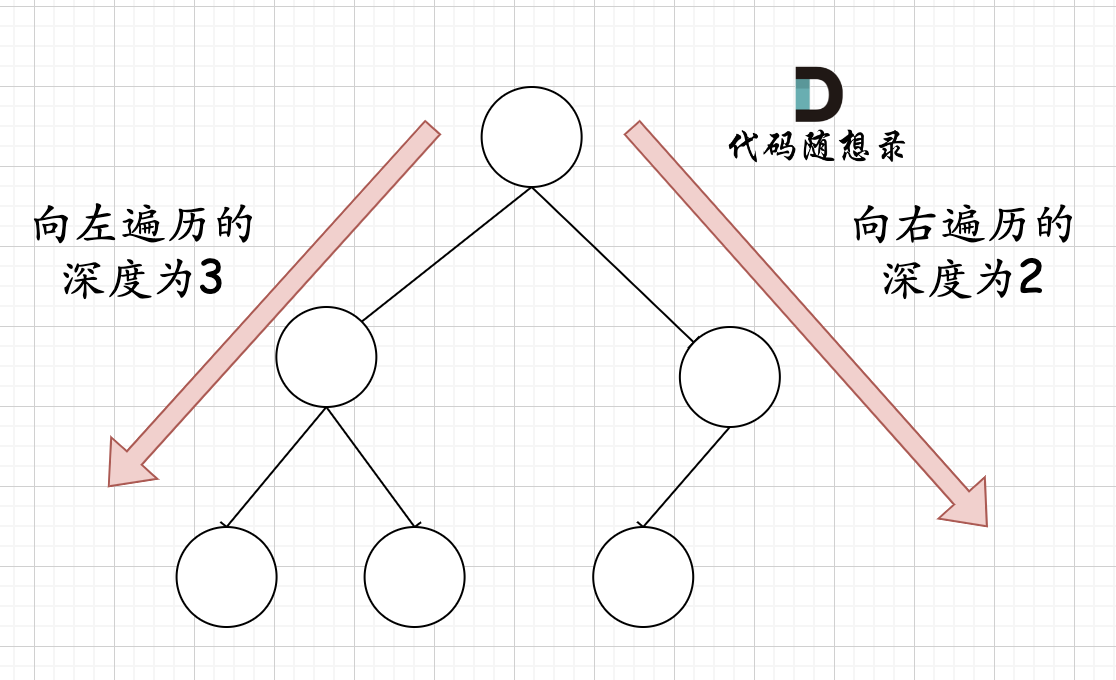
注意如果有疑问：递归向左遍历的深度等于递归向右遍历的深度，但也不是满二叉树。就像下图所示：

这就陷入了误区，这棵二叉树，它根本就不是一个完全二叉树！

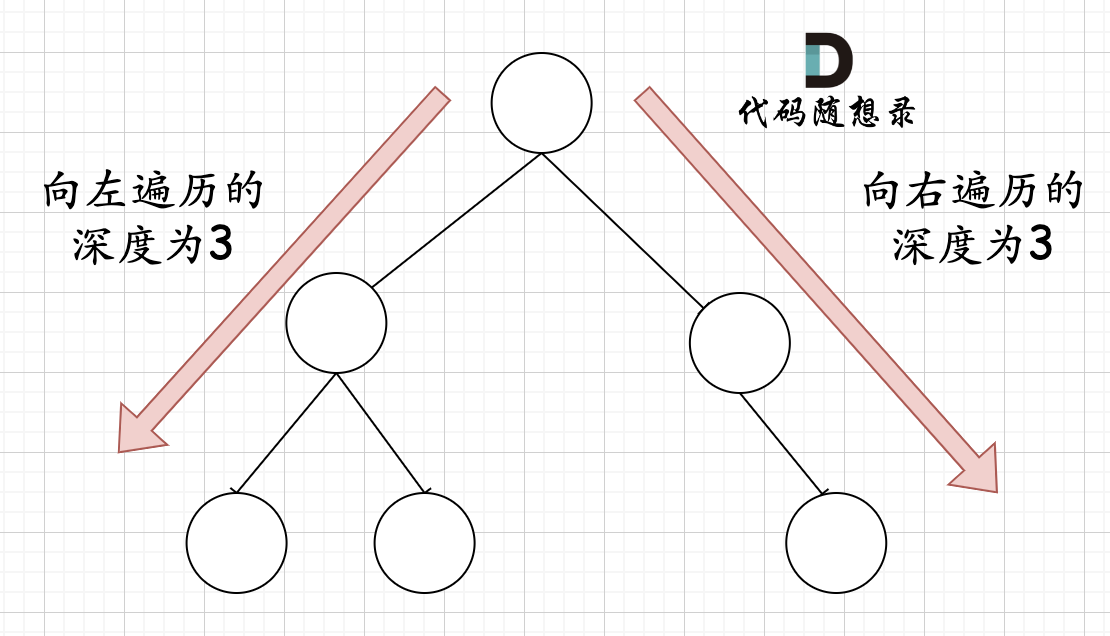
4代码

代码的思路是通过递归来计算完全二叉树的节点数。

首先判断根节点是否为空，若为空则返回0。

然后分别求出左子树和右子树的深度。如果左子树深度等于右子树深度，则说明是满二叉树，此时可以直接用公式计算节点数。

如果左子树深度不等于右子树深度，则说明左子树是完全二叉树，此时递归计算左子树和右子树的节点数，再加上根节点的1即可。

class Solution {
public:// 定义一个函数 countNodes，参数为二叉树的根节点int countNodes(TreeNode* root) {// 如果根节点为空，则返回0if (root ==  nullptr) return 0;// 定义左右子树指针，并初始化为根节点的左右子树TreeNode* left = root->left;TreeNode* right = root->right;// 定义左右子树深度，并初始化为0int leftDepth = 0, rightDepth = 0;// 计算左子树的深度while (left) {left = left->left;leftDepth++;}// 计算右子树的深度while (right) {right = right->right;rightDepth++;}// 如果左右子树深度相同，说明是一棵满二叉树，直接返回节点数if (leftDepth == rightDepth) return (2<left);int rightNum = countNodes(root->right);// 计算当前根节点及其左右子树的节点数int result = leftNum +rightNum +1;// 返回结果return result;}
};