《【Chatgpt】+【simplelatex】再也不用愁数学公式！！！》

1. 使用OCR工具解析公式：SimpleTex

示例：

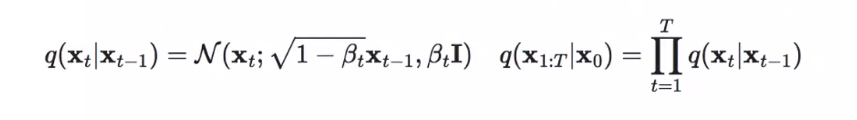
q(\mathbf x_t|\mathbf x_{t-1})=\mathcal N(\mathbf x_t;\sqrt{1-\beta_t}\mathbf x_{t-1},\beta_t\mathbf I)\quad q(\mathbf x_{1:T}|\mathbf x_0)=\prod\limits_{t=1}^T q(\mathbf x_t|{\mathbf x}_{t-1})\quad

2. 询问ChatGPT公式的含义

示例提示：

请解释如下公式：q(\mathbf x_t|\mathbf x_{t-1})=\mathcal N(\mathbf x_t;\sqrt{1-\beta_t}\mathbf x_{t-1},\beta_t\mathbf I)\quad q(\mathbf x_{1:T}|\mathbf x_0)=\prod\limits_{t=1}^T q(\mathbf x_t|{\mathbf x}_{t-1})\quad

示例输出：

这些公式是针对状态空间模型中的一个重要概率分布，即高斯分布（也称为正态分布）的一般形式。在状态空间模型中，高斯分布用于描述系统状态的不确定性，并且通常假定其满足马尔科夫性质，即当前状态只依赖于前一个状态。

公式中的 N(xt;1−βtxt−1,βtI)\mathcal N(\mathbf x_t;\sqrt{1-\beta_t}\mathbf x_{t-1},\beta_t\mathbf I)N(xt​;1−βt​​xt−1​,βt​I) 表示高斯分布的一般形式，其中 xt\mathbf x_txt​ 是当前状态的值，xt−1\mathbf x_{t-1}xt−1​ 是前一个状态的值，βt\beta_tβt​ 是一个常数（通常小于1），I\mathbf II 是单位矩阵。这个高斯分布的均值是 1−βtxt−1\sqrt{1-\beta_t}\mathbf x_{t-1}1−βt​​xt−1​，表示当前状态的值以前一个状态的值为中心，而方差是 βtI\beta_t\mathbf Iβt​I，表示当前状态的值的不确定性。

公式中的 q(x1:T∣x0)=∏t=1Tq(xt∣xt−1)q(\mathbf x_{1:T}|\mathbf x_0)=\prod\limits_{t=1}^T q(\mathbf x_t|{\mathbf x}{t-1})q(x1:T​∣x0​)=t=1∏T​q(xt​∣xt−1) 表示根据前一个状态的值，生成当前状态的概率密度函数，这个概率密度函数是一个由 TTT 个条件概率密度函数的连乘积组成的形式。在这个连乘积中，每个条件概率密度函数 q(xt∣xt−1)q(\mathbf x_t|{\mathbf x}{t-1})q(xt​∣xt−1) 都表示在给定前一个状态 xt−1\mathbf x_{t-1}xt−1​ 的情况下，生成当前状态 xt\mathbf x_txt​ 的概率密度函数。在这个公式中，假定状态满足马尔科夫性质，即当前状态只依赖于前一个状态，因此 q(xt∣xt−1)q(\mathbf x_t|{\mathbf x}{t-1})q(xt​∣xt−1) 只依赖于前一个状态 xt−1\mathbf x{t-1}xt−1。