磁效应的来源
本文是学习以后的备忘,水平有限,如果出现错误,请理解。
不带’的参数均为静止参照系X的参数,带’的均为运动参照系X’的参数。
一、洛伦兹变换
令k=1−u2/c2k=\sqrt{1-u^2/c^2}k=1−u2/c2
:x′=x−utkx'=\frac{x-ut}{k}x′=kx−ut
y′=yy'=yy′=y
z′=zz'=zz′=z
:t′=t−ux/c2kt'=\frac{t-ux/c^2}{k}t′=kt−ux/c2
二、速度的变换
vx′=dx′dt′=dx−udtdt−uc2dx=vx−u1−uc2vxv'_x=\frac{dx'}{dt'}=\frac{dx-udt}{dt-\frac{u}{c^2}dx}=\frac{v_x-u}{1-\frac{u}{c^2}v_x}vx′=dt′dx′=dt−c2udxdx−udt=1−c2uvxvx−u
vy′=dy′dt′=kdydt−uc2dx=kvy1−uc2vxv'_y=\frac{dy'}{dt'}=k\frac{dy}{dt-\frac{u}{c^2}dx}=k\frac{v_y}{1-\frac{u}{c^2}v_x}vy′=dt′dy′=kdt−c2udxdy=k1−c2uvxvy
vz′=dz′dt′=kdzdt−uc2dx=kvz1−uc2vxv'_z=\frac{dz'}{dt'}=k\frac{dz}{dt-\frac{u}{c^2}dx}=k\frac{v_z}{1-\frac{u}{c^2}v_x}vz′=dt′dz′=kdt−c2udxdz=k1−c2uvxvz
三 动量的变换
由m′=m01−v′2c2m'=\frac{m_0}{\sqrt{1-\frac{v'^2}{c^2}}}m′=1−c2v′2m0和m=m01−v2c2m=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}m=1−c2v2m0得m′=m1−v2c21−v′2c2m'=m\frac{\sqrt{1-\frac{v^2}{c^2}}}{\sqrt{1-\frac{v'^2}{c^2}}}m′=m1−c2v′21−c2v2
现在要把v′v'v′和vx′v'_xvx′用K系变量替代。
v′2=vx′2+vy′2+vz′2=(vx−u)2+(kvy)2+(kvz)2(1−uc2vx)2v'^2=v'^2_x+v'^2_y+v'^2_z=\frac{(v_x-u)^2+(kv_y)^2+(kv_z)^2}{(1-\frac{u}{c^2}v_x)^2}v′2=vx′2+vy′2+vz′2=(1−c2uvx)2(vx−u)2+(kvy)2+(kvz)2
化简得1−v′2c2=k1−v2c21−uc2vx\sqrt{1-\frac{v'^2}{c^2}}=\frac{k\sqrt{1-\frac{v^2}{c_2}}}{1-\frac{u}{c^2}v_x}1−c2v′2=1−c2uvxk1−c2v2
因此Px′=m′vx′=mk(1−uc2vx)vx′=mk(vx−u)=Px−uc2EkP'_x=m'v'_x=\frac{m}{k}(1-\frac{u}{c^2}v_x)v'_x=\frac{m}{k}(v_x-u)=\frac{P_x-\frac{u}{c^2}E}{k}Px′=m′vx′=km(1−c2uvx)vx′=km(vx−u)=kPx−c2uE
Py′=PyP'_y=P_yPy′=Py
Pz′=PzP'_z=P_zPz′=Pz
四、力的变换
fx′=dPx′dt′=(需要把K′系变量变成K系变量,化简后)=fx−uc2fyvy−uc2fzvzf'_x=\frac{dP'_x}{dt'}=(需要把K'系变量变成K系变量,化简后)=f_x-\frac{u}{c^2}f_yv_y-\frac{u}{c^2}f_zv_zfx′=dt′dPx′=(需要把K′系变量变成K系变量,化简后)=fx−c2ufyvy−c2ufzvz
fy′=(需要把K′系变量变成K系变量,化简后)=kfy1−uc2vxf'_y=(需要把K'系变量变成K系变量,化简后)=\frac{kf_y}{1-\frac{u}{c^2}v_x}fy′=(需要把K′系变量变成K系变量,化简后)=1−c2uvxkfy
fz′=(需要把K′系变量变成K系变量,化简后)=kfz1−uc2vxf'_z=(需要把K'系变量变成K系变量,化简后)=\frac{kf_z}{1-\frac{u}{c^2}v_x}fz′=(需要把K′系变量变成K系变量,化简后)=1−c2uvxkfz
五、磁效应的来源
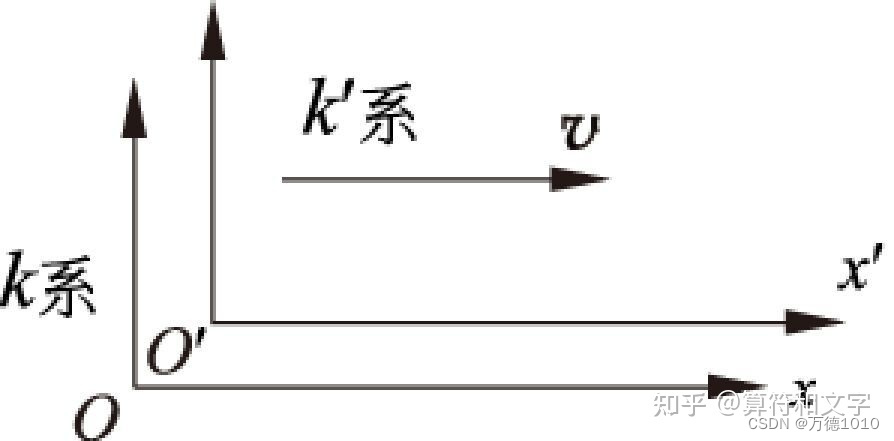
上图,为计算方便,假设此时两坐标系原点重合。K’系以速度u相对K系向x轴正方向运动。q0q_0q0在原点处,相对K系静止,q1q_1q1在r(rx,ry,rz)r(r_x,r_y,r_z)r(rx,ry,rz)处。相对K系以速度v1((v1)x,(v1)y,(v1)z)v_1((v_1)_x,(v_1)_y,(v_1)_z)v1((v1)x,(v1)y,(v1)z)运动.。现在考察q1的受力情况q_1的受力情况q1的受力情况
fx′=fx−uc2fyvy−uc2fzvzf'_x=f_x-\frac{u}{c^2}f_yv_y-\frac{u}{c^2}f_zv_zfx′=fx−c2ufyvy−c2ufzvz
其中uc2fyvy=uc2Eyq1vy=uc2q04πe0ry2q1vy\frac{u}{c^2}f_yv_y=\frac{u}{c^2}E_yq_1v_y=\frac{u}{c^2}\frac{q_0}{4\pi e_0r^2_y}q_1v_yc2ufyvy=c2uEyq1vy=c2u4πe0ry2q0q1vy
因为1c2=μ0e0\frac{1}{c^2}=\mu_0 e_0c21=μ0e0
所以uc2fyvy=q1vy(μ0uq04πry2)\frac{u}{c^2}f_yv_y=q_1v_y(\frac{\mu_0uq_0}{4\pi r^2_y})c2ufyvy=q1vy(4πry2μ0uq0)
同理,uc2fzvz=q1vz(μ0uq04πrz2)\frac{u}{c^2}f_zv_z=q_1v_z(\frac{\mu_0uq_0}{4\pi r^2_z})c2ufzvz=q1vz(4πrz2μ0uq0)
则fx′=fx−q1vy(μ0uq04πry2)−q1vz(μ0uq04πrz2)f'_x=f_x-q_1v_y(\frac{\mu_0uq_0}{4\pi r^2_y})-q_1v_z(\frac{\mu_0uq_0}{4\pi r^2_z})fx′=fx−q1vy(4πry2μ0uq0)−q1vz(4πrz2μ0uq0)
同样计算得,
fy′=fyk1−uc2vx=fyk(1+uvx′c2)=fyk+q1vx′q0μ0u4πry2kf'_y=\frac{f_yk}{1-\frac{u}{c^2}v_x}=\frac{f_y}{k}(1+\frac{uv'_x}{c^2})=\frac{f_y}{k}+q_1v'_x\frac{q_0\mu _0u}{4\pi r^2_yk}fy′=1−c2uvxfyk=kfy(1+c2uvx′)=kfy+q1vx′4πry2kq0μ0u
fz′=fzk1−uc2vx=fzk(1+uvx′c2)=fzk+q1vx′q0μ0u4πrz2kf'_z=\frac{f_zk}{1-\frac{u}{c^2}v_x}=\frac{f_z}{k}(1+\frac{uv'_x}{c^2})=\frac{f_z}{k}+q_1v'_x\frac{q_0\mu _0u}{4\pi r^2_zk}fz′=1−c2uvxfzk=kfz(1+c2uvx′)=kfz+q1vx′4πrz2kq0μ0u
注意的是,这里第一个式子用的是K系速度vy,vzv_y,v_zvy,vz,第二第三个式子使用了以下三个式子把K系速度换成了K‘系速度vy′,vz′v'_y,v'_zvy′,vz′。
vx=vx′+u1+uc2vx′v_x=\frac{v'_x+u}{1+\frac{u}{c^2}v'_x}vx=1+c2uvx′vx′+u
vy=kvy′1+uc2vx′v_y=k\frac{v'_y}{1+\frac{u}{c^2}v'_x}vy=k1+c2uvx′vy′
vz=kvz′1+uc2vx′v_z=k\frac{v'_z}{1+\frac{u}{c^2}v'_x}vz=k1+c2uvx′vz′
上述关于fx′,fy′,fz′f'_x,f'_y,f'_zfx′,fy′,fz′三个式子的意思是,当一个带电粒子q0q_0q0以速度uuu向x轴负方向运动时,以速度v’运动的带电粒子q1q_1q1在q0q_0q0产生的电场中的受力为f′(fx+q1(vy+vz)Bx,fy+q1vx′Byk,fz+q1vx′Bzk)f'(f_x+q_1(v_y+v_z)B_x,\frac{f_y+q_1v'_xB_y}{k}, \frac{f_z+q_1v'_xB_z}{k})f′(fx+q1(vy+vz)Bx,kfy+q1vx′By,kfz+q1vx′Bz),
其中Bi=q0μ0u4πri2B_i=\frac{q_0 \mu_0 u}{4\pi r^2_i}Bi=4πri2q0μ0u
上一篇:一天吃透MySQL锁面试八股文