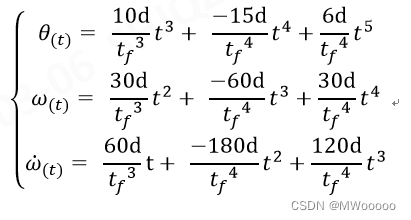机器人姿态规划的三种常见方法:欧拉角、角轴和四元数
参考文献:
1. 布鲁诺·西西里安诺等[意] 《机器人学:建模、规划与控制》
2. 四元数小总结 - 孤独の巡礼 - 博客园 (cnblogs.com)
3. 基于单位四元数的姿态插补(Matlab) - 知乎 (zhihu.com)
4. 基于四元数的工业机器人姿态规划与插补算法的研究 - 豆丁网Docin
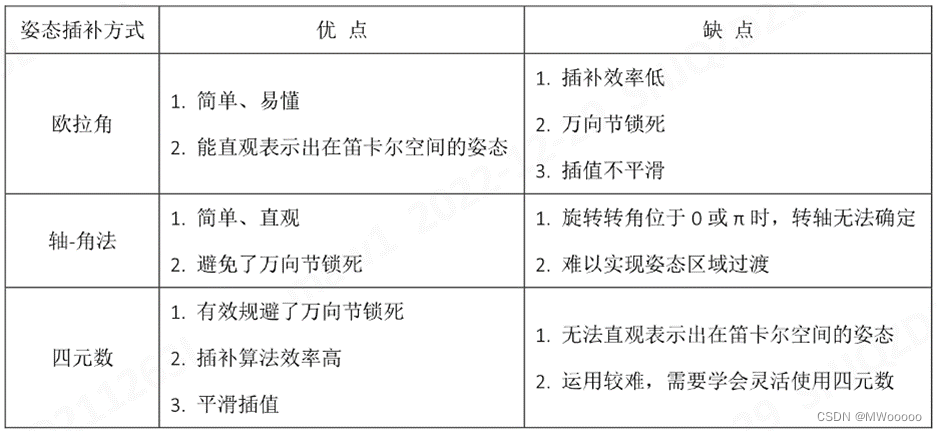
本文总结了用于机器人姿态规划的常见三种姿态规划方法,包括:欧拉角、角轴以及四元数。三种方法各有优劣,根据使用场景自由选择。
欧拉角
通过为欧拉角欧拉角ϕ= (φ,θ,ψ) 指定时间律来描述指向。通常使用三次多项式或混合抛物线线性分段时间律是方便的。基于这种方法,时变坐标系的角速度将具有连续量。
例子:
已知条件:初始和目标欧拉角已知,初始速度、加速度为0,最终速度、加速度为0。插值时间为tf。使用五次多项式时间律可以满足条件,位置、速度、加速度均连续。
有插值公式:
但是欧拉角姿态规划的方法存在万向节锁死的问题。
角轴


对于定义在操作空间的误差变量(位置和方向)进行处理,其表达式由下式给出:
其中,![]() 表示末端执行器的期望值,
表示末端执行器的期望值,![]() 表示末端执行器的计算值。
表示末端执行器的计算值。
对于涉及到方向误差的部分,其表达式取决于末端执行器方向的详细表示,即,欧拉角,角和轴,单位四元数。
对于初始旋转矩阵![]() 和目标旋转矩阵
和目标旋转矩阵![]() ,有:
,有:
所以有,
对于旋转变换![]() ,可以表示为绕空间中一固定轴的旋转矩阵。计算轴的单位向量
,可以表示为绕空间中一固定轴的旋转矩阵。计算轴的单位向量![]() 和
和![]() ,可以求得初始旋转矩阵绕该轴的角速度和角加速度。
,可以求得初始旋转矩阵绕该轴的角速度和角加速度。
其中,轴的单位向量![]() :
:
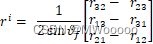
![]()
为![]() 指定一个时间律,当
指定一个时间律,当![]() ,且有
,且有![]() 。我们使用五次多项式插值为
。我们使用五次多项式插值为![]() 指定时间律,其中,
指定时间律,其中,![]() 为总的姿态运动时间,由人为指定。
为总的姿态运动时间,由人为指定。
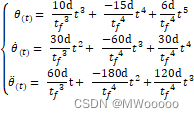
![]() 为常量,由此得到的速度和加速度为:
为常量,由此得到的速度和加速度为:
最后,为了表征末端执行器关于基坐标系的指向轨迹,需要进行如下变化:
由此我们可以获取机械臂的姿态关节的运动速度,再通过雅可比逆解到各个关节。
但是以上基于角轴表达式的姿态规划存在奇异问题,当 ![]() = 0或
= 0或 ![]() = Π时,单位向量r是奇异的。我们对
= Π时,单位向量r是奇异的。我们对![]() = 0这种场景进行了特殊处理。当
= 0这种场景进行了特殊处理。当![]() = 0时,默认姿态无转动,强制规划各姿态关节速度为0。
= 0时,默认姿态无转动,强制规划各姿态关节速度为0。![]() = Π时尚未做处理,后续考虑进行补充优化。
= Π时尚未做处理,后续考虑进行补充优化。
四元数
1. 四元数基础公式



2. 四元数球面线性插值
2.1 四元数球面线性插值的基本概念:
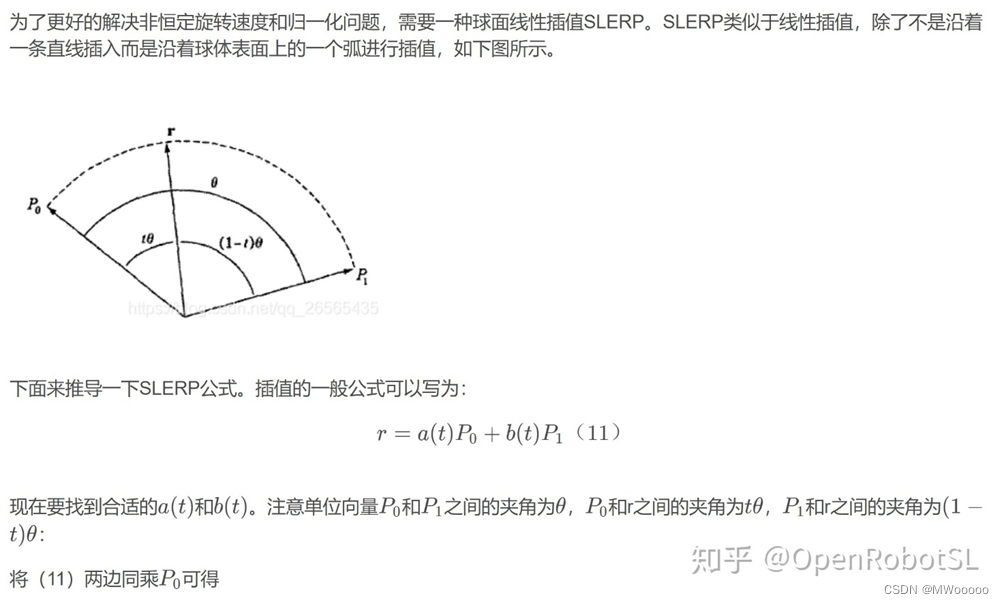


2.2 四元数球面线性插值的基本公式

我们采用第二种构造方式进行姿态规划!