文章目录

• 1、题目一：邮局选址
• • 1.1 题目描述
  • 1.2 思路分析
  • 1.3 代码实现
• 2、题目二：K蛋问题
• • 2.1 题目描述
  • 2.2 思路分析
  • 2.3 代码实现
  • 2.4 最优解解法
  • 2.5 对数器

1、题目一：邮局选址

1.1 题目描述

一条直线上有居民点，邮局只能建在居民点上。

给定一个 有序正数 数组arr，每个值表示居民点的一维坐标，再给定一个正数 num，表示邮局数量。

选择 num 个居民点建立 num 个邮局，使得所有的居民点到最近邮局的总距离最短，返回最短的距离。

例：

arr = [1, 2, 3, 4, 5, 1000]， num = 2
第一个邮局建立在 3 位置，第二个邮局建立在 1000 位置。那么1位置到邮局的距离为2，
2位置到邮局的距离为1，
3位置到邮局的距离为0，
4位置到邮局的距离为1，
5位置到邮局的距离为2，
1000位置到邮局的距离为0.这种方案下的总距离为6，其他任何方案的总距离都不会比该方案的总距离更短，所以返回6

1.2 思路分析

首先来看个简单的问题：在L到R范围上，只建一个邮局，建在哪里使得所有居民点到该邮局的总距离最短。

生成一个预处理结构，该结构可以知道任意 LLL 到 RRR 范围上，只建一个邮局的最小代价。

结论：在有序数组中，邮局建在中点位置一定是最优的；偶数个点时，无论建在上中点，还是下中点，总代价相同。

对于 aaa 到 bbb 范围，知道邮局应该建在中点位置，但是如何求解所有点到该邮局的距离，如果暴力求解太慢，所以需要优化。

假设通过这种枚举优化可以得到一个预处理结构 WWW，其中 W[L][R]W[L][R]W[L][R] 表示 LLL 到 RRR 范围上如果只建一个邮局的最优代价。

主流程的思想和『画家问题』一样：0 ~ iii 范围的居民点由 jjj 个邮局负责，枚举最后一个邮局负责的居民点范围。

定义 dp[i][j]dp[i][j]dp[i][j] 为 0 ~ iii 范围的居民点由 jjj 个邮局负责的最小代价。

例 dp[7][3]dp[7][3]dp[7][3] 分配方式：

• [0,7] 由 2 个邮局负责，最后一个邮局什么都不做，则代价为 dp[7][2]dp[7][2]dp[7][2]；
• [0,6] 由 2 个邮局负责，最后一个邮局负责 [7,7]，则代价为 dp[6][2]+W[7][7]dp[6][2] + W[7][7]dp[6][2]+W[7][7]；
• [0,5] 由 2 个邮局负责，最后一个邮局负责 [6, 7]，则代价为 dp[5][2]+W[6][7]dp[5][2] + W[6][7]dp[5][2]+W[6][7]；
• …
• 前 2 个邮局什么都不做，最后一个邮局负责[0,7]，则代价为 W[0][7]W[0][7]W[0][7]。

所有情况都枚举了，相当于划分点从0到7每个位置都进行尝试，最优答案一定在其中。

1.3 代码实现

import java.util.Arrays;public class PostOfficeProblem {//O(N^3)：枚举没有优化public static int min1(int[] arr, int num) {if (arr == null || num < 1 || arr.length < num) {return 0;}int N = arr.length;//w的范围为(N+1)*(N+1），之所以要多一个位置，是为了避免边界讨论//因为假设居民点范围为0~7，如果前k-1个邮局负责0~7，则最后1个邮局实际上没有负责任何范围//但是可以认为最后1个邮局负责了8~7这个范围，该范围是无效的，此时就是w[8][7]，会返回0，而避免了边界讨论int[][] w = new int[N + 1][N + 1]; //w[L][R] 表示从L到R范围建立1个邮局的最优代价//for循环只填了表的右上部分，因为这个部分是L for (int R = L + 1; R < N; R++) {w[L][R] = w[L][R - 1] + arr[R] - arr[(L + R) >> 1];}}int[][] dp = new int[N][num + 1]; //dp[i][k] 表示从0~i范围建立k个邮局的最优代价//dp表第0行表示0~0范围上建k个邮局，代价都为0，所以跳过//填第1列，直接从w中取值for (int i = 0; i < N; i++) { dp[i][1] = w[0][i]; //0~i范围，建1个邮局的代价就是w[0][i]}for (int i = 1; i < N; i++) {//居民点枚举 for (int j = 2; j <= Math.min(i, num); j++) { //邮局数量枚举 j>i无意义，代价为0; j>num也无意义，限制了邮局个数int ans = Integer.MAX_VALUE;for (int k = 0; k <= i; k++) { //划分点枚举，没有做任何优化ans = Math.min(ans, dp[k][j - 1] + w[k + 1][i]); //[0,k]范围由前j-1个邮局负责，[k+1,i]由最后1个邮局负责}dp[i][j] = ans;}}return dp[N - 1][num];}//邮局问题符合四边形不等式的特征：//1. 两个参数（i表示范围，j表示邮局数量）的区间划分问题 //2. 每个格子有枚举行为//3. 固定一个参数，另一个参数与答案存在单调关系；//4. 且呈反向单调关系  （范围i固定，j↑，代价↓；j ↓，代价↑。邮局数量j固定，i↑，代价↑；i↓，代价↓）//5. 是否能获得枚举指导的位置对：//分析位置依赖：假设0~7范围建立3个邮局，即dp[7][3]//那么，可以划分的情况：// ① 0~7 2个邮局，最后1个邮局不用，则依赖dp[7][2]；// ② 0~6 2个邮局，7 最后1个邮局，则依赖于dp[6][2]；// ③ 0~5 2个邮局，6~7 最后1个邮局，则依赖于dp[5][2]// ......//dp[7][3] 依赖于它的前一列//所以可以取得 「左+下」 的位置对//最优解O(N^2)：优化了枚举public static int min2(int[] arr, int num) {if (arr == null || num < 1 || arr.length < num) {return 0;}int N = arr.length;int[][] w = new int[N + 1][N + 1];for (int L = 0; L < N; L++) {for (int R = L + 1; R < N; R++) {w[L][R] = w[L][R - 1] + arr[R] - arr[(L + R) >> 1];}}int[][] dp = new int[N][num + 1];int[][] best = new int[N][num + 1];for (int i = 0; i < N; i++) {dp[i][1] = w[0][i];best[i][1] = -1;}for (int j = 2; j <= num; j++) { //枚举邮局数量for (int i = N - 1; i >= j; i--) {int down = best[i][j - 1]; //下限，由左侧提供int up = i == N - 1 ? N - 1 : best[i + 1][j]; //上限，由下侧提供int ans = Integer.MAX_VALUE;int bestChoose = -1;for (int leftEnd = down; leftEnd <= up; leftEnd++) {int leftCost = leftEnd == -1 ? 0 : dp[leftEnd][j - 1];int rightCost = leftEnd == i ? 0 : w[leftEnd + 1][i];int cur = leftCost + rightCost;if (cur <= ans) { //注意：不同于画家问题，这里<=都能通过，关于是<还是<=，和四边形不等式的证明有关，而我们不证明，直接使用对数器进行验证尝试ans = cur;bestChoose = leftEnd;}}dp[i][j] = ans;best[i][j] = bestChoose;}}return dp[N - 1][num];}// for testpublic static int[] randomSortedArray(int len, int range) {int[] arr = new int[len];for (int i = 0; i != len; i++) {arr[i] = (int) (Math.random() * range);}Arrays.sort(arr);return arr;}// for testpublic static void printArray(int[] arr) {for (int i = 0; i != arr.length; i++) {System.out.print(arr[i] + " ");}System.out.println();}// for testpublic static void main(String[] args) {int N = 30;int maxValue = 100;int testTime = 10000;System.out.println("测试开始");for (int i = 0; i < testTime; i++) {int len = (int) (Math.random() * N) + 1;int[] arr = randomSortedArray(len, maxValue);int num = (int) (Math.random() * N) + 1;int ans1 = min1(arr, num);int ans2 = min2(arr, num);if (ans1 != ans2) {printArray(arr);System.out.println(num);System.out.println(ans1);System.out.println(ans2);System.out.println("Oops!");}}System.out.println("测试结束");}
}

2、题目二：K蛋问题

2.1 题目描述

一座大楼有 0 ~ NNN 层，地面算作第 0 层，最高的一层为第 NNN 层。

已知鸡蛋从第 0 层掉落肯定不会摔碎，从第 iii 层掉落可能会摔碎，也可能不会摔碎（1≤i≤N1 \le i \le N1≤i≤N)。

给定整数 NNN 作为楼层数，再给定整数 KKK 作为鸡蛋数，返回如果想找到鸡蛋不会摔碎的最高层数，即使在最差的情况下扔的最少次数。一次只能扔一个鸡蛋。

• 例1

N = 10, K=1返回10。
因为只有1个鸡蛋，所以不得不从第1层开始一直试到第 10 层，在最差的情况下，即第 10 层是不会摔碎的最高层，最少也要扔 10 次。

• 例2

N = 3, K = 2返回2。
先在 2 层扔 1 个鸡蛋，如果碎了，试第 1 层，如果没碎，试第 3 层。

• 例3

N = 105, K = 2返回 14。
第一个鸡蛋先在 14 层扔，碎了则用仅存的一个鸡蛋试 1~13；
若没碎，第一个鸡蛋继续在 27 层扔，碎了则用仅存的一个鸡蛋试 15~26。 
若没碎，第一个鸡蛋继续在 39 层扔，碎了则用仅存的一个鸡蛋试 28~38。 
若没碎，第一个鸡蛋继续在 50 层扔，碎了则用仅存的一个鸡蛋试 40~49。
若没碎，第一个鸡蛋继续在 60 层扔， 碎了则用仅存的一个鸡蛋试 51~59。 
若没碎，第一个鸡蛋继续在 69 层扔，碎了则用仅存的一个鸡蛋试 61~68。 
若没碎，第一个鸡蛋继续在 77 层扔，碎了则用仅存的一个鸡蛋试 70~76。 
若没碎，第一个鸡蛋继续在 84 层 扔，碎了则用仅存的一个鸡蛋试 78~83。 
若没碎，第一个鸡蛋继续在 90 层扔，碎了则用仅存的一个鸡蛋试 85~89。 
若没碎，第一个鸡蛋继续在 95 层扔，碎了则用仅存的一个鸡蛋试 91~94。 
若没碎，第一个鸡蛋继续 在 99 层扔，碎了则用仅存的一个鸡蛋试 96~98。 
若没碎，第一个鸡蛋继续在 102 层扔，碎了则用仅存的一 个鸡蛋试 100、101。 
若没碎，第一个鸡蛋继续在 104 层扔，碎了则用仅存的一个鸡蛋试 103。 
若没碎，第 一个鸡蛋继续在 105 层扔，若到这一步还没碎，那么 105 便是结果。

2.2 思路分析

定义一个递归函数f(int N,int K)，第一个参数表示还有多少层楼需要试，第二个参数表示还剩多少个蛋，返回最差情况下要扔的次数。

以第 1 个鸡蛋扔哪层来进行可能性的划分。

f(100, 3) 可能性的枚举：

• 如果第1个鸡蛋先在 1 层扔，碎了则表示0层是最高的不会摔碎的楼层；没碎，则还剩99层需要尝试，即 f(99, 3)。因为是最差情况下扔的次数：max{0, f(99,3)} + 1 (+1表示为当前扔的这一次，max{}表示后续还要扔的次数)
• 如果第1个鸡蛋先在 2 层扔，碎了则还有1层楼需要试，还剩2个蛋，f(1, 2)；没碎，还剩98层需要试，即 f(98,3)。最差情况下扔的次数：max{f(1, 2), f(98, 3)} + 1
• … …
• 如果第1个鸡蛋先在 iii 层扔，碎了则还有 1 ~ (i−1)(i-1)(i−1) 一共 (i−1)(i-1)(i−1) 层需要，还剩2个蛋，即f(i-1, 2)；没碎，还剩 (100 - iii) 层需要试，即f(100-i, 3)。最差情况下会返回最差的答案：max{f(i-1,2), f(100-i, 3)} + 1

枚举 iii 就能得到最后的答案。

很明显，这是一个二维动态规划。

restN 表示还剩的楼层数，restK 表示还剩的鸡蛋数。

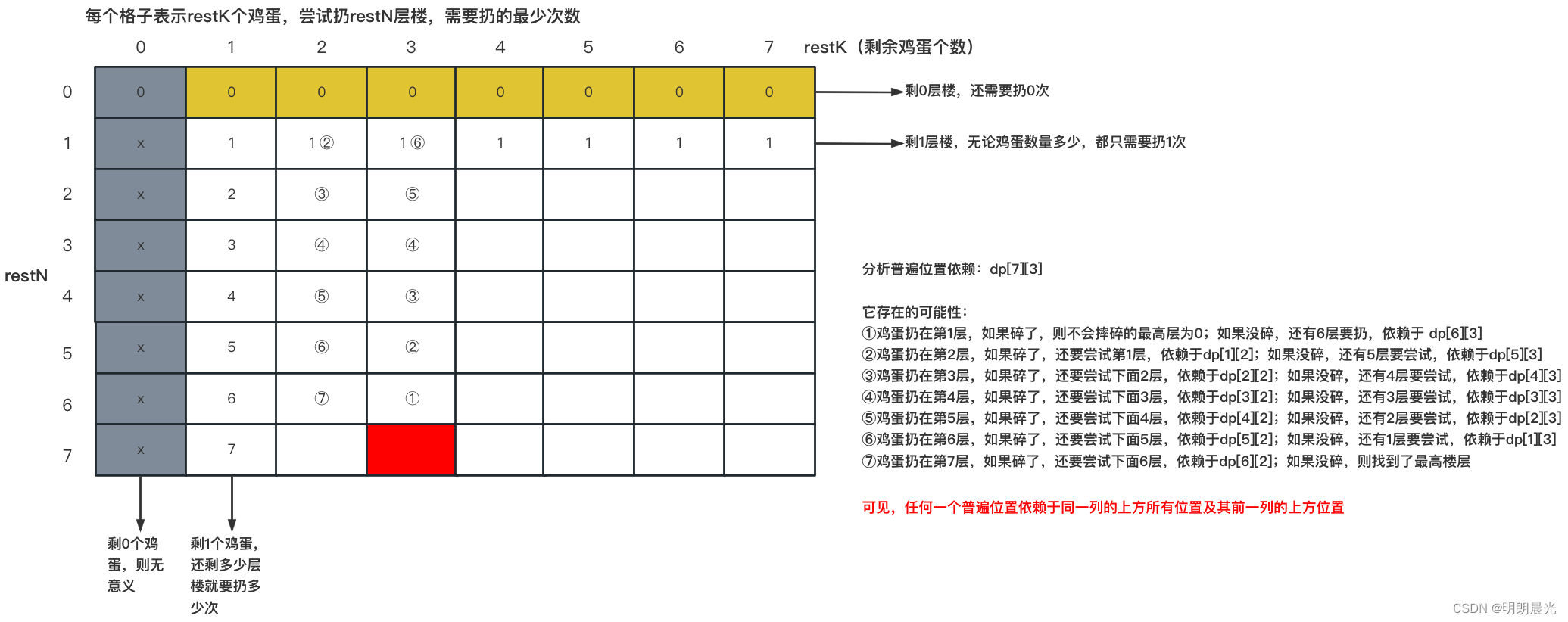
考察是否满足四边形不等式技巧特征：

1. 是两个参数的区间划分问题 【楼层数 和 鸡蛋数】
2. 每个格子有枚举行为 【如上图普遍位置的分析】
3. 存在可变参数固定一个，另一个参数与答案是单调关系，且为反向单调关系。【如果固定鸡蛋数，楼层数变少↓，答案扔的次数变少↓；楼层数变多↑，答案扔的次数变多↑。如果固定楼层数，鸡蛋数变少↓，扔的次数变多↑；鸡蛋数变多↑，扔的次数变少↓。注意是两个参数各自与答案的关系是反向的，两对关系是反向的】
4. 根据位置依赖可知可以获得枚举指导的位置对 “上 + 右” 【求解整张表的时候，从上往下依次求每行，而每行从右往左计算。如此一来，最右的位置无法获得指导位置，而其他的位置既有上，又有右】

2.3 代码实现

// leetcode测试链接：https://leetcode.com/problems/super-egg-drop
// 方法1和方法2会超时
// 方法3勉强通过
// 方法4打败100%
public class ThrowChessPiecesProblem {public static int superEggDrop1(int kChess, int nLevel) {if (nLevel < 1 || kChess < 1) {return 0;}return Process1(nLevel, kChess);}// rest还剩多少层楼需要去验证// k还有多少颗棋子能够使用// 一定要验证出最高的不会碎的楼层！但是每次都是坏运气。// 返回至少需要扔几次？public static int Process1(int rest, int k) {if (rest == 0) {return 0;}if (k == 1) {return rest;}int min = Integer.MAX_VALUE;for (int i = 1; i != rest + 1; i++) { // 第一次扔的时候，仍在了i层min = Math.min(min, Math.max(Process1(i - 1, k - 1), Process1(rest - i, k)));}return min + 1;}// 没有任何枚举优化// kChess表示k个鸡蛋，nLevel表示n层楼public static int superEggDrop2(int kChess, int nLevel) {if (nLevel < 1 || kChess < 1) {return 0;}//只有1个鸡蛋，则有多少层要扔多少次if (kChess == 1) { return nLevel;}//dp表，楼层数为行，鸡蛋数为列int[][] dp = new int[nLevel + 1][kChess + 1];for (int i = 1; i != dp.length; i++) { //只有1个鸡蛋dp[i][1] = i;}for (int i = 1; i != dp.length; i++) {for (int j = 2; j != dp[0].length; j++) {int min = Integer.MAX_VALUE;for (int k = 1; k != i + 1; k++) { //枚举鸡蛋第1次在哪层楼扔，枚举没有进行优化min = Math.min(min, Math.max(dp[k - 1][j - 1], dp[i - k][j])); //因为是最差情况，所以要求max，然后再在得到的结果里找最小值}dp[i][j] = min + 1; //+1为当前扔的这次}}return dp[nLevel][kChess];}//四边形不等式技巧：有枚举优化public static int superEggDrop3(int kChess, int nLevel) {if (nLevel < 1 || kChess < 1) {return 0;}if (kChess == 1) {return nLevel;}int[][] dp = new int[nLevel + 1][kChess + 1];for (int i = 1; i != dp.length; i++) {dp[i][1] = i;}//best的意义：如果100层楼，3个鸡蛋，最后证明第1个鸡蛋在15层扔的时候能得到最优解，则best[100][3]=15int[][] best = new int[nLevel + 1][kChess + 1];for (int i = 1; i != dp[0].length; i++) {dp[1][i] = 1;best[1][i] = 1; //只剩1层楼，i个鸡蛋，则最优方案就是在剩余楼层的第1层扔}// 从上往下填每行：第2行，第3行，....// 每行从右往左填for (int i = 2; i < nLevel + 1; i++) { //枚举行，从上往下for (int j = kChess; j > 1; j--) { //从右往左填每行，因为要取 「上 + 右」位置对int ans = Integer.MAX_VALUE;int bestChoose = -1;int down = best[i - 1][j]; //下限，来自上方int up = j == kChess ? i : best[i][j + 1]; //上限，来自右方。j == kChess，即是最右的位置，不优化for (int first = down; first <= up; first++) { //枚举剩余的鸡蛋中第1个鸡蛋要在剩余楼层中第1次在哪层扔int cur = Math.max(dp[first - 1][j - 1], dp[i - first][j]);if (cur <= ans) { //注意：此处必须是<= ans = cur;bestChoose = first;}}dp[i][j] = ans + 1;best[i][j] = bestChoose;}}return dp[nLevel][kChess];}
}

2.4 最优解解法

规定dp表的行为鸡蛋数，列为扔的次数，定义dp[i][j] 表示的是最差情况下，iii 个鸡蛋扔 jjj 次，能解决多少层楼的问题。

xxx 个鸡蛋，扔0次，则无意义；-> 第0列无意义
xxx 个鸡蛋，扔1次，能解决1层楼的问题；->第1列全是1
1个鸡蛋扔 mmm 次，就能解决 mmm 层楼的问题（ m>=1m>=1m>=1 ) ->第1行是自然序列 1 2 3 4 …

在dp表的列往右增长过程中，当 dp[i][j]>=给定的楼层数 时，则此时的 「列」 就是答案

将该表从左往右按列从上往下填，什么时候超过给定的楼层，此时对应的列就是答案。

普遍位置的依赖问题：如果 7 个鸡蛋，扔 10 次，能解决多少层楼的问题呢？

假设 6 个鸡蛋扔 9 次 能解决 50 层楼的问题（客观事实），7个鸡蛋扔9次能解决55层楼的问题（客观事实），那么 7 个鸡蛋扔 10 次能解决 106 层楼的问题，为啥呢？

假设有 nnn 层楼，任何一层都可能是答案，即是最高的不会摔碎的楼层。假设鸡蛋第1次在 mmm 层楼扔，如果碎了，剩 6 个鸡蛋，还能扔 9 次，因为这是在 7 个鸡蛋扔 10 次的情况下出现的摔碎的可能性，此时只要下方的楼层数在50以内，就能被 6个鸡蛋扔9次（即dp[6][9]） 这个子问题解决；如果没碎，还剩 7 个鸡蛋，还能扔 9 次，即dp[7][9]，因为鸡蛋没有碎，于是就要往上方找，而因为7个鸡蛋扔9次能解决 55 层楼的问题，所以此时只要上方楼层在 55 层以内，就能被7个鸡蛋扔10次这个子问题解决掉。所以能解决 50 + 55 + 1 = 106层，+1就是m这一层。

所以任何一个普遍位置 = 它左边的格子 + 左上方的格子 + 1，两项相加致使该表增长极快，可以迅速到达题目给定的楼层数。

不用提前准备多少列，因为普遍位置只依赖于其邻居左边和左上方，所以只需要一列，空间压缩，复用一列即可，实质上就是一维数组。

public class ThrowChessPiecesProblem {// leetcode测试链接：https://leetcode.com/problems/super-egg-drop// 方法5打败100%，方法5是在方法4的基础上做了进一步的常数优化//最优解public static int superEggDrop4(int kChess, int nLevel) {if (nLevel < 1 || kChess < 1) {return 0;}int[] dp = new int[kChess];int res = 0; //当前到了哪一列while (true) {res++;int previous = 0;for (int i = 0; i < dp.length; i++) { //每列从上往下填，枚举鸡蛋个数 int tmp = dp[i];dp[i] = dp[i] + previous + 1;previous = tmp;if (dp[i] >= nLevel) {return res;}}}}//最优解，优化了常数项public static int superEggDrop5(int kChess, int nLevel) {if (nLevel < 1 || kChess < 1) {return 0;}int bsTimes = log2N(nLevel) + 1;if (kChess >= bsTimes) {return bsTimes;}int[] dp = new int[kChess];int res = 0;while (true) {res++;int previous = 0;for (int i = 0; i < dp.length; i++) {int tmp = dp[i];dp[i] = dp[i] + previous + 1;previous = tmp;if (dp[i] >= nLevel) {return res;}}}}public static int log2N(int n) {int res = -1;while (n != 0) {res++;n >>>= 1;}return res;}
}

2.5 对数器

public class ThrowChessPiecesProblem {public static void main(String[] args) {int maxN = 500;int maxK = 30;int testTime = 1000;System.out.println("测试开始");for (int i = 0; i < testTime; i++) {int N = (int) (Math.random() * maxN) + 1;int K = (int) (Math.random() * maxK) + 1;int ans2 = superEggDrop2(K, N);int ans3 = superEggDrop3(K, N);int ans4 = superEggDrop4(K, N);int ans5 = superEggDrop5(K, N);if (ans2 != ans3 || ans4 != ans5 || ans2 != ans4) {System.out.println("出错了!");}}System.out.println("测试结束");}
}