该系列博客主要讲述Matlab软件在自动控制方面的应用，如无自动控制理论基础，请先学习自动控制系列博文，该系列博客不再详细讲解自动控制理论知识。
自动控制理论基础相关链接：https://blog.csdn.net/qq_39032096/category_10287468.html?spm=1001.2014.3001.5482
博客参考书籍：《MATLAB/Simulink与控制系统仿真》。

2.其他根轨迹及综合实例分析

2.1 其他形式根轨迹

2.1.1 参数根轨迹

• 除根轨迹增益K∗K^*K∗为变化参数的根轨迹外，其他情形下的根轨迹统称为广义根轨迹；如：系统的参数根轨迹，开环传递函数中零点个数多于极点个数的根轨迹，零度根轨迹；
• 将负反馈系统中K∗K^*K∗变化时的根轨迹称为常规根轨迹；
• 以非开环增益为可变参数绘制的根轨迹称为参数根轨迹；

设系统闭环特征方程为：
1+G(s)H(s)=01+G(s)H(s)=0 1+G(s)H(s)=0
进行等效变换：
AP(s)Q(s)=−1A\frac{P(s)}{Q(s)}=-1 AQ(s)P(s)​=−1
其中：AAA为除K∗K^*K∗外，系统任意变化参数，P(s)、Q(s)P(s)、Q(s)P(s)、Q(s)为两个与AAA无关的首一多项式；

上两式相等，即：
Q(s)+AP(s)=1+G(s)H(s)=0Q(s)+AP(s)=1+G(s)H(s)=0 Q(s)+AP(s)=1+G(s)H(s)=0
可得等效单位系统，其等效开环传递函数为
G1(s)H1(s)=AP(s)Q(s)G_1(s)H_1(s)=A\frac{P(s)}{Q(s)} G1​(s)H1​(s)=AQ(s)P(s)​
利用上式绘制的根轨迹就是参数AAA变化时的参数根轨迹；

2.1.2 零度根轨迹

• 如果研究的控制系统为非最小相位系统，则不能采用常规根轨迹的法则绘制系统根轨迹，其相角遵循0°+2kπ0°+2k\pi0°+2kπ条件，而不是180°+2kπ180°+2k\pi180°+2kπ条件，因此称为零度根轨迹；
• 非最小相位系统指在sss右半平面具有开环零极点的控制系统；
• 零度根轨迹来源：一是非最小相位系统中包含sss最高次幂的系数为负的因子；二是控制系统中包含正反馈内回路；

【零度根轨迹绘制法则】

• 【法则1】：根轨迹的起点和终点。

  • 根轨迹起于开环极点，终于开环零点；

• 【法则2】：根轨迹的分支数、对称性和连续性。

  • 根轨迹的分支数与开环有限零点数mmm和有限极点数nnn中的大者相等，根轨迹是连续且对称于实轴；

• 【法则3】：根轨迹的渐近线。

  • 当开环有限极点数nnn大于有限零点数mmm时，有n−mn-mn−m条根轨迹分支沿着与实轴交角为φa\varphi_aφa​、交点为σa\sigma_aσa​的一组渐近线趋于无穷远处，且有：
    φa=2kπn−m,k=0,1,2,⋯,n−m−1；σa=∑i=1npi−∑j=1mzjn−m\varphi_a=\frac{2k\pi}{n-m},k=0,1,2,\cdots,n-m-1；\sigma_a=\frac{\displaystyle\sum_{i=1}^np_i-\displaystyle\sum_{j=1}^mz_j}{n-m} φa​=n−m2kπ​,k=0,1,2,⋯,n−m−1；σa​=n−mi=1∑n​pi​−j=1∑m​zj​​

• 【法则4】：根轨迹在实轴上的分布。

  • 实轴上的某一区域，若其右边开环实数零、极点个数之和为偶数，则该区域必是根轨迹。

• 【法则5】：根轨迹的分离点与分离角。

  • 两条或两条以上根轨迹分支在sss平面上相遇又立即分开的点，称为根轨迹分离点，分离点坐标ddd：
    ∑j=1m1d−zj=∑i=1n1d−pi\sum_{j=1}^{m}\frac{1}{d-z_j}=\sum_{i=1}^n\frac{1}{d-p_i} j=1∑m​d−zj​1​=i=1∑n​d−pi​1​
    其中：zjz_jzj​为开环零点，pip_ipi​为开环极点；

    分离角为：(2k+1)π/l(2k+1)\pi/l(2k+1)π/l；

  • 如果根轨迹位于实轴上两个相邻的开环极点间，其中一个可以是无限极点，则这两个极点间至少存在一个分离点；

  • 如果根轨迹位于实轴上两个相邻的开环零点间，其中一个可以是无限零点，则这两个零点间至少存在一个分离点；

  • 由两个极点和一个有限零点组成的开环系统，只要有限零点没有位于两个实数极点间，当K∗K^*K∗从零变化到无穷时，闭环根轨迹的复数部分，是以有限零点为圆心，以有限零点到分离点的距离为半径的一个圆，或圆的一部分；

• 【法则6】：根轨迹的起始角和终止角。

  • 根轨迹离开开环复数极点处的切线与正实轴的夹角，称为起始角，记为：θpi\theta_{p_i}θpi​​；

  • 根轨迹进入开环复数零点处的切线与正实轴的夹角，称为终止角，记为：φzi\varphi_{z_i}φzi​​；

  • 起始角和终止角的计算：
    θpi=2kπ+(∑j=1mφzjpi−∑j=1(j≠i)nθpjpi)；k=0，±1，±2，⋯φzi=2kπ−(∑j=1(j≠i)mφzjzi−∑j=1nθpjzi)；k=0，±1，±2，⋯\begin{aligned} &\theta_{p_i}=2k\pi+(\sum_{j=1}^m\varphi_{z_jp_i}-\sum_{j=1\\(j≠i)}^n\theta_{p_jp_i})；k=0，±1，±2，\cdots\\\\ &\varphi_{z_i}=2k\pi-(\sum_{j=1\\(j≠i)}^m\varphi_{z_jz_i}-\sum_{j=1}^n\theta_{p_jz_i})；k=0，±1，±2，\cdots \end{aligned} ​θpi​​=2kπ+(j=1∑m​φzj​pi​​−j=1(j=i)∑n​θpj​pi​​)；k=0，±1，±2，⋯φzi​​=2kπ−(j=1(j=i)∑m​φzj​zi​​−j=1∑n​θpj​zi​​)；k=0，±1，±2，⋯​

• 【法则7】：根轨迹与虚轴的交点。

  • 若根轨迹与虚轴相交，则交点上的K∗K^*K∗值和ω\omegaω值可用劳斯判据确定，亦可令闭环特征方程的s=jωs={\rm j}\omegas=jω，令其实部和虚部为零求解；

  • 若根轨迹与虚轴相交，表示闭环系统存在纯虚根，即K∗K^*K∗的数值使闭环系统处于临界稳定状态，可令劳斯表第一列中包含K∗K^*K∗的项为零，即可确定根轨迹与虚轴交点上的K∗K^*K∗值；

  • 令闭环特征方程的s=jωs={\rm j\omega}s=jω代入闭环特征方程，可得：
    1+G(jω)H(jω)=01+G({\rm j}\omega)H({\rm j}\omega)=0 1+G(jω)H(jω)=0
    令其实部和虚部均等于000即可求解其参数，有：
    {Re[1+G(jω)H(jω)]=0Im[1+G(jω)H(jω)]=0\begin{cases} &{\rm Re}[1+G({\rm j}\omega)H({\rm j}\omega)]=0\\ &{\rm Im}[1+G({\rm j}\omega)H({\rm j}\omega)]=0 \end{cases} {​Re[1+G(jω)H(jω)]=0Im[1+G(jω)H(jω)]=0​

• 【法则8】：根之和。

  • 当n−m≥2n-m≥2n−m≥2时，特征方程第二项系数与K∗K^*K∗无关，无论K∗K^*K∗取何值，开环nnn个极点之和总是等于闭环特征方程nnn个根之和，即：
    ∑i=1nsi=∑i=1npi\sum_{i=1}^ns_i=\sum_{i=1}^np_i i=1∑n​si​=i=1∑n​pi​

2.2 其他形式根轨迹实例

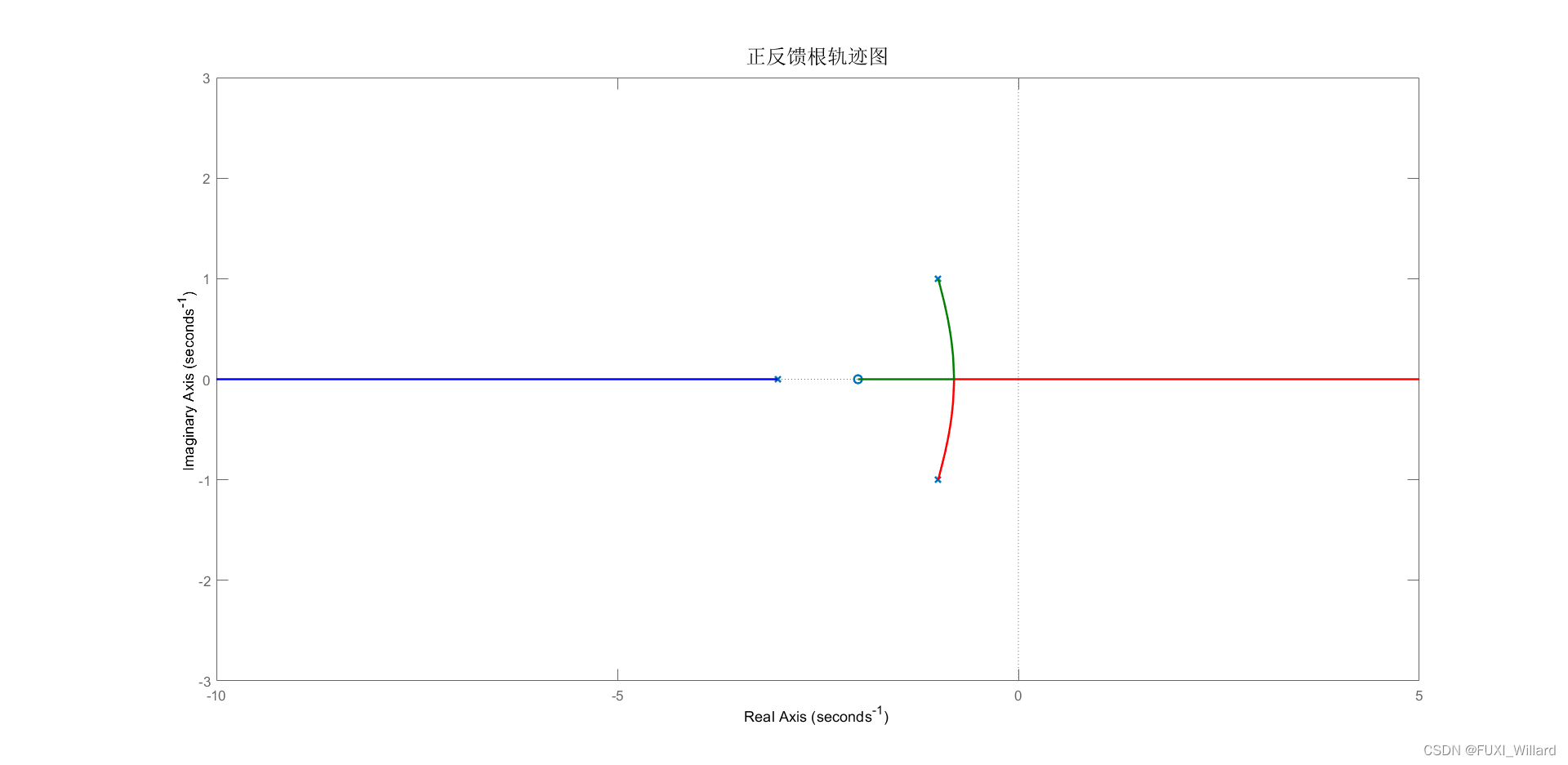
2.2.1 实例1：正反馈轨迹

实验要求：绘制正反馈系统的根轨迹，已知单位反馈系统开环传递函数G(s)H(s)=K(s+2)(s+3)(s2+2s+2)，G(s)H(s)=\displaystyle\frac{K(s+2)}{(s+3)(s^2+2s+2)}，G(s)H(s)=(s+3)(s2+2s+2)K(s+2)​，其中K<0K<0K<0，使用MATLAB{\rm MATLAB}MATLAB绘制系统的根轨迹。

解：

% 实例Chapter6.2.2.1
clc;clear;% 建立控制系统模型
num=[1,2];den=conv([1,3],[1,2,2]);
sys=tf(num,den);% 绘制根轨迹
rlocus(-sys);axis([-10 5 -3 3]);
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('正反馈根轨迹图','FontSize',15);

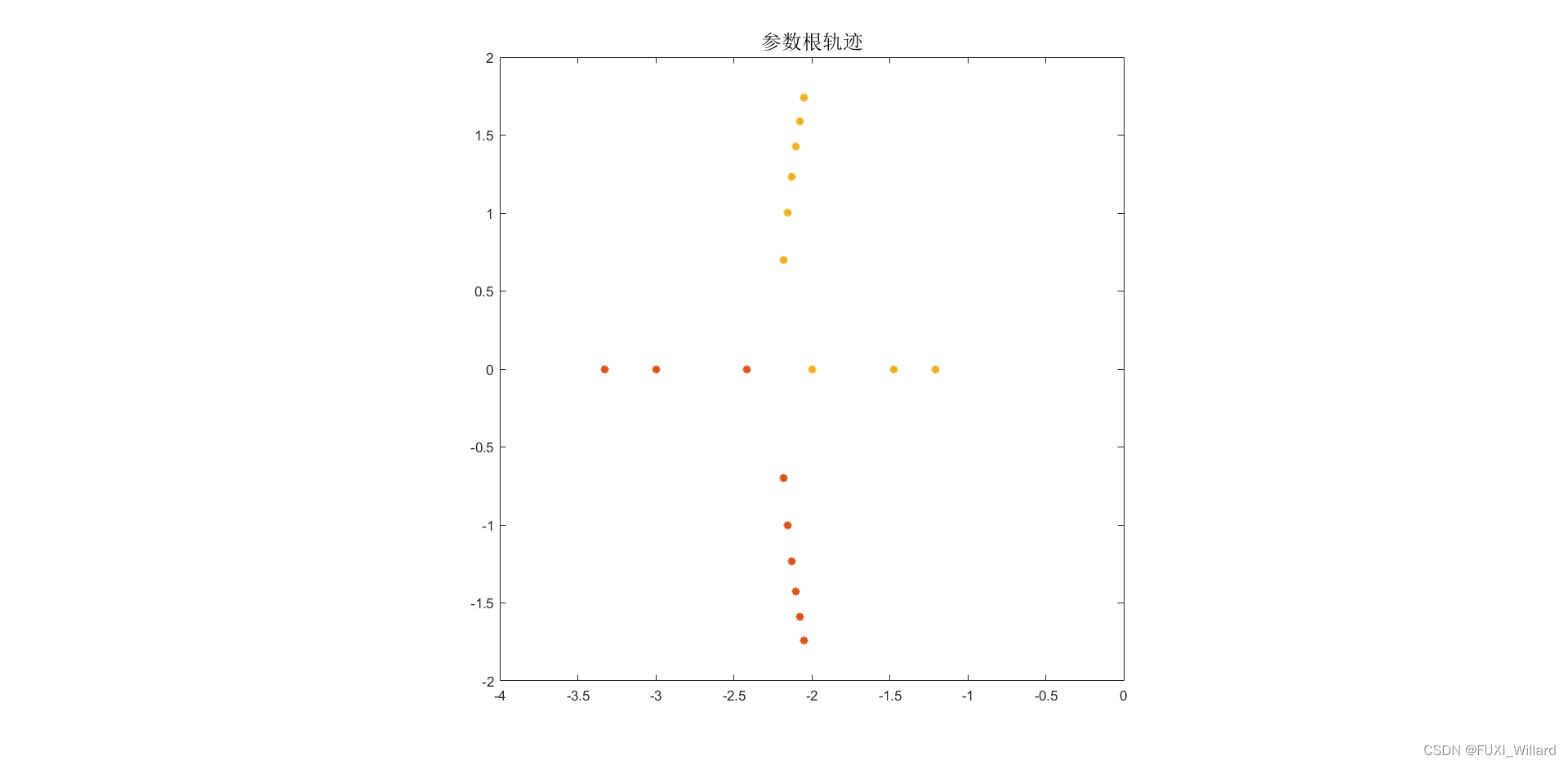
2.2.2 实例2：参数根轨迹

实验要求：已知某单位负反馈系统开环传递函数为：G(s)H(s)=5(s+a)(s+1)(s+3)(s+12)G(s)H(s)=\displaystyle\frac{5(s+a)}{(s+1)(s+3)(s+12)}G(s)H(s)=(s+1)(s+3)(s+12)5(s+a)​，其中：2≤a≤102≤a≤102≤a≤10,使用MATLAB{\rm MATLAB}MATLAB绘制参数aaa的根轨迹。

解：

% 实例Chapter6.2.2.2
clc;clear;% 定义变量
K=5;den=conv([1,1],conv([1,3],[1,12]));% 定义数组存储结果
clpoles=[];param=[];% a值从2变化到10
for a=2:10num=[0,0,K,K*a];clpoly=num+den;clp=roots(clpoly);clpoles=[clpoles;clp'];param=[param;a];
end% 打印a和极点表格
disp([param,clpoles]);% 绘制极点
plot(clpoles,'*');
axis equal;axis([-4,0,-2,2]);
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('参数根轨迹','FontSize',15);

% 极点表格：2.0000 + 0.0000i -11.4658 + 0.0000i  -3.3291 + 0.0000i  -1.2051 + 0.0000i3.0000 + 0.0000i -11.5249 + 0.0000i  -3.0000 + 0.0000i  -1.4751 + 0.0000i4.0000 + 0.0000i -11.5826 + 0.0000i  -2.4174 + 0.0000i  -2.0000 + 0.0000i5.0000 + 0.0000i -11.6388 + 0.0000i  -2.1806 - 0.6972i  -2.1806 + 0.6972i6.0000 + 0.0000i -11.6938 + 0.0000i  -2.1531 - 1.0041i  -2.1531 + 1.0041i7.0000 + 0.0000i -11.7475 + 0.0000i  -2.1262 - 1.2341i  -2.1262 + 1.2341i8.0000 + 0.0000i -11.8001 + 0.0000i  -2.1000 - 1.4251i  -2.1000 + 1.4251i9.0000 + 0.0000i -11.8516 + 0.0000i  -2.0742 - 1.5913i  -2.0742 + 1.5913i10.0000 + 0.0000i -11.9020 + 0.0000i  -2.0490 - 1.7399i  -2.0490 + 1.7399i

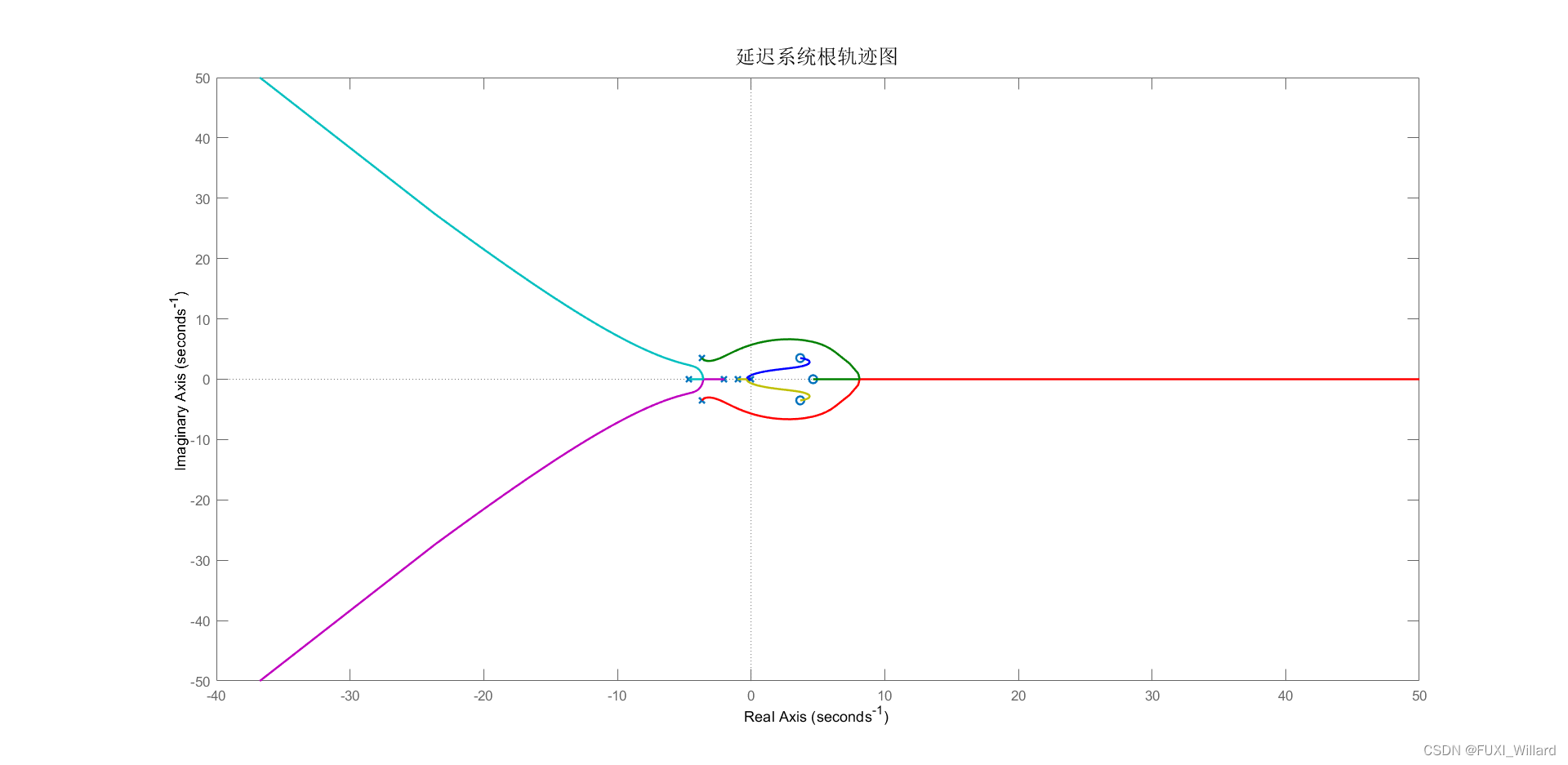
2.2.3 实例3：延迟系统根轨迹

实验要求：已知某单位负反馈系统的开环传递函数为：G(s)H(s)=1s(s+1)(0.5s+1)e−sG(s)H(s)=\displaystyle\frac{1}{s(s+1)(0.5s+1)}{\rm e}^{-{s}}G(s)H(s)=s(s+1)(0.5s+1)1​e−s，使用MATLAB{\rm MATLAB}MATLAB绘制该延迟系统的根轨迹。

解：

% 实例Chapter6.2.2.3
clc;clear;% 建立控制系统模型
num=[0,1];den=conv([1,0],conv([1,1],[0.5,1]));
sys1=tf(num,den);% 对延迟环节进行Pade近似
[np,dp]=pade(1,3);
sys=sys1*tf(np,dp);% 绘制根轨迹
rlocus(sys);
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('延迟系统根轨迹图','FontSize',15);

2.3 控制系统性能分析

2.3.1 闭环零极点与时间响应

• 系统的动态性能基本上由接近虚轴的闭环极点确定，这样的极点，称为主导极点；
• 主导极点定义为对整个时间响应过程起主要作用的闭环极点；
• 时间响应分量的消逝速度，除取决于相应闭环极点的实部值外，还与该极点处的留数，即闭环零、极点之间的相互位置有关；
• 只有既接近虚轴，又不十分接近闭环零点的闭环极点，才可能成为主导极点；
• 如果闭环零、极点相距很近，那么这样的闭环零、极点常称为偶极子；偶极子有实数偶极子和复数偶极子之分，复数偶极子必共轭出现；只要偶极子不十分接近坐标原点，它们对系统的影响甚微，可以忽略它们的存在；
• 接近坐标原点的偶极子对系统动态性能的影响必须考虑；不论偶极子接近坐标原点的程度如何，并不影响系统主导极点的地位；
• 确定偶极子法则：如果闭环零、极点之间的距离比它们本身模值小一个数量级，则这一对闭环零、极点就构成偶极子；
• 采用主导极点代替系统全部闭环极点来估算系统性能指标的方法，称为主导极点法；采用主导极点时，在全部闭环极点中，选留最靠近虚轴而又不十分靠近闭环零点的一个或几个闭环极点作为主导极点，略去不十分接近原点的偶极子，以及比主导极点距虚轴远六倍以上的闭环零、极点；

2.3.2 系统性能定性分析

闭环系统零、极点位置对时间响应性能的影响总结：

• 稳定性。如果闭环极点全部位于sss左半平面，则系统一定是稳定的，即稳定性只与闭环极点位置有关，与闭环零点无关；
• 运动形式。如果闭环系统无零点，且闭环极点均为实数极点，则时间响应一定是单调的；如果闭环极点均为复数极点，则时间响应一般是振荡的；
• 超调量。超调量主要取决于闭环复数主导极点的衰减率σ1/ωd=ζ/1−ζ2\sigma_1/\omega_d=\zeta/\sqrt{1-\zeta^2}σ1​/ωd​=ζ/1−ζ2​，并与其他闭环零、极点接近坐标原点的程度有关；
• 调节时间。调节时间主要取决于最靠近虚轴的闭环复数极点的实部绝对值σ1=ζωn\sigma_1=\zeta\omega_nσ1​=ζωn​；如果实数极点距虚轴最近，且附近没有实数零点，则调节时间主要取决于该实数极点的模值；
• 实数零、极点影响。零点减小系统阻尼，使峰值时间提前，超调量增大；极点增大系统阻尼，使峰值时间滞后，超调量减小；它们的作用，随着本身接近坐标原点的程度而加强；
• 偶极子及其处理。如果零、极点之间的距离比它们本身的模值小一个数量级，则构成偶极子；远离原点的偶极子影响可忽略，接近原点的偶极子影响必须考虑；
• 主导极点。在sss平面上，最靠近虚轴而附近没有闭环零点的一些闭环极点，对系统性能影响最大，称为主导极点；凡比主导极点实部大3～6倍以上的其他闭环零、极点影响可忽略；
• 闭环实数主导极点对系统性能的影响：闭环实数主导极点作用相当于增大系统的阻尼，使峰值时间滞后，超调量下降；如果实数极点比共轭复数极点更接近坐标原点，甚至可以使振荡过程变为非振荡过程；

2.4 综合实例分析

实验要求：已知单位负反馈控制系统开环传递函数为：G(s)H(s)=K(s+1)s(s−1)(s+4)G(s)H(s)=\displaystyle\frac{K(s+1)}{s(s-1)(s+4)}G(s)H(s)=s(s−1)(s+4)K(s+1)​，要求：

1. 绘制此控制系统的根轨迹；
2. 确定使闭环系统稳定的KKK值；
3. 分析此控制系统的阶跃响应性能；
4. 利用rltool{\rm rltool}rltool对系统的性能进行分析；

解：

【STEP1{\rm STEP1}STEP1】：建立此控制系统的数学模型。

% STEP1：建立控制系统的模型
num=[1,1];den=conv([1,0],conv([1,-1],[1,4]));
sys=tf(num,den);sys

% 控制系统模型输出：
sys = s + 1-----------------s^3 + 3 s^2 - 4 s

【STEP2{\rm STEP2}STEP2】：绘制该控制系统根轨迹。

% STEP2：绘制控制系统根轨迹
rlocus(sys);grid on;
set(findobj(get(gca,'Children'),'LineWidth',0.5),'LineWidth',1.5);
title('控制系统根轨迹图','FontSize',15);% 计算用户选定点处的增益和其他闭环极点
[k,poles]=rlocfind(sys)

% 在根轨迹图上点击根轨迹与虚轴交点，输出如下：
k =6.0267poles =-2.9951 + 0.0000i-0.0024 + 1.4185i-0.0024 - 1.4185i

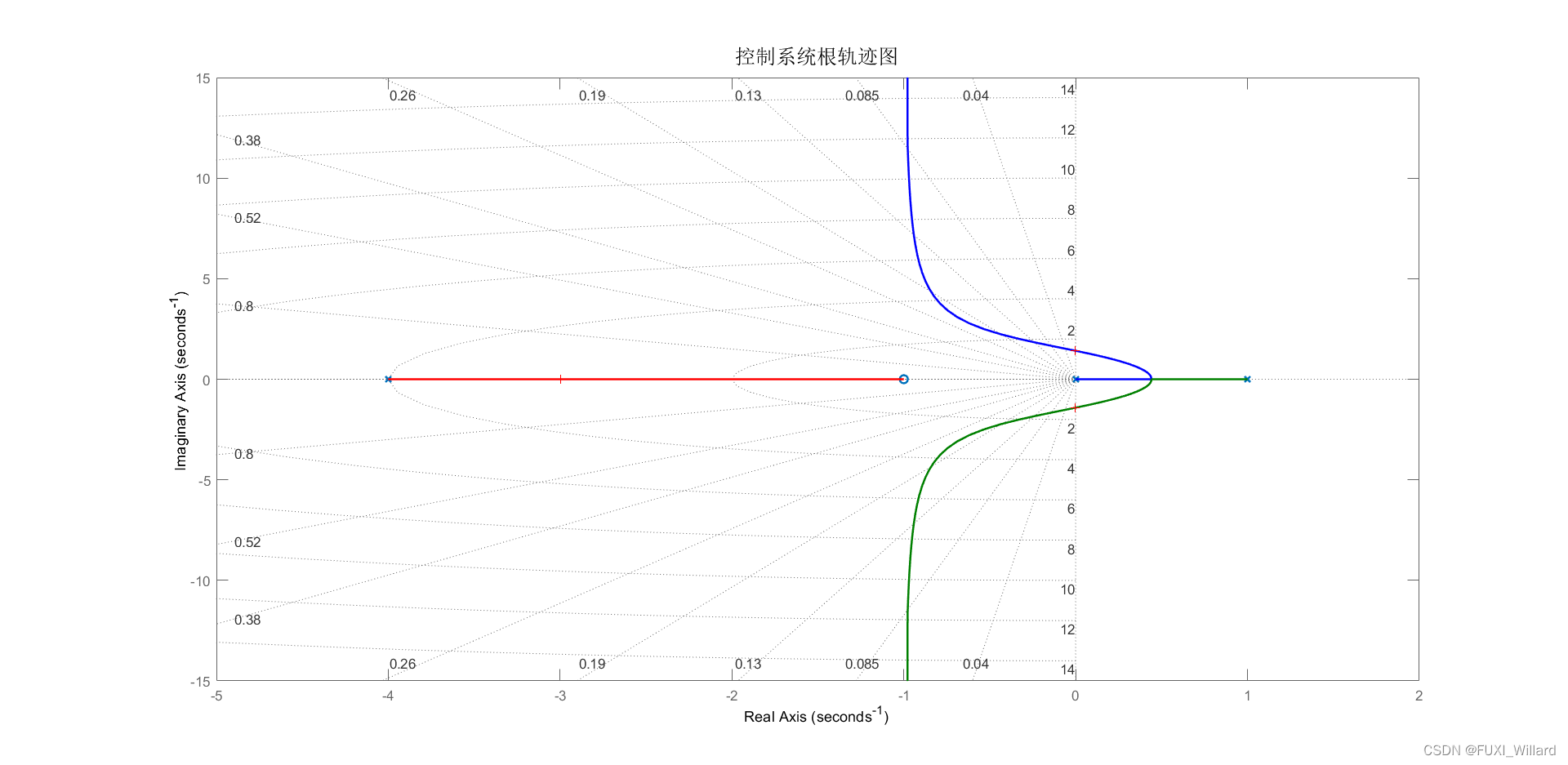
• 当增益K>6K>6K>6时，闭环控制系统所有极点均位于虚轴的左半部分，此时系统稳定；

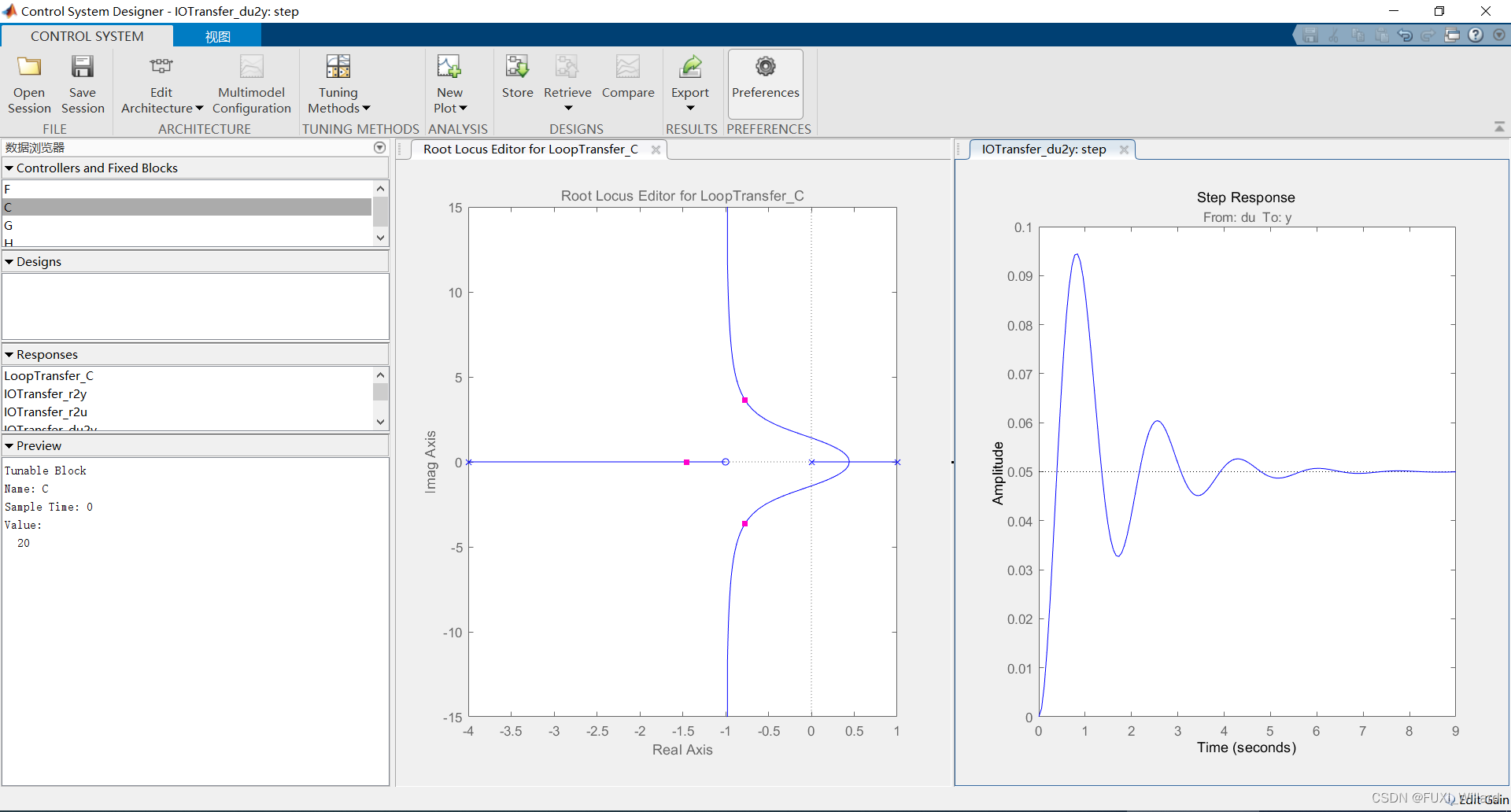
【STEP3{\rm STEP3}STEP3】：使用rltool{\rm rltool}rltool工具分析。

% STEP3：使用rltool工具分析
rltool(sys)% 在rltool工具中，设置C的值为6
% New Plot中选择绘制STEP响应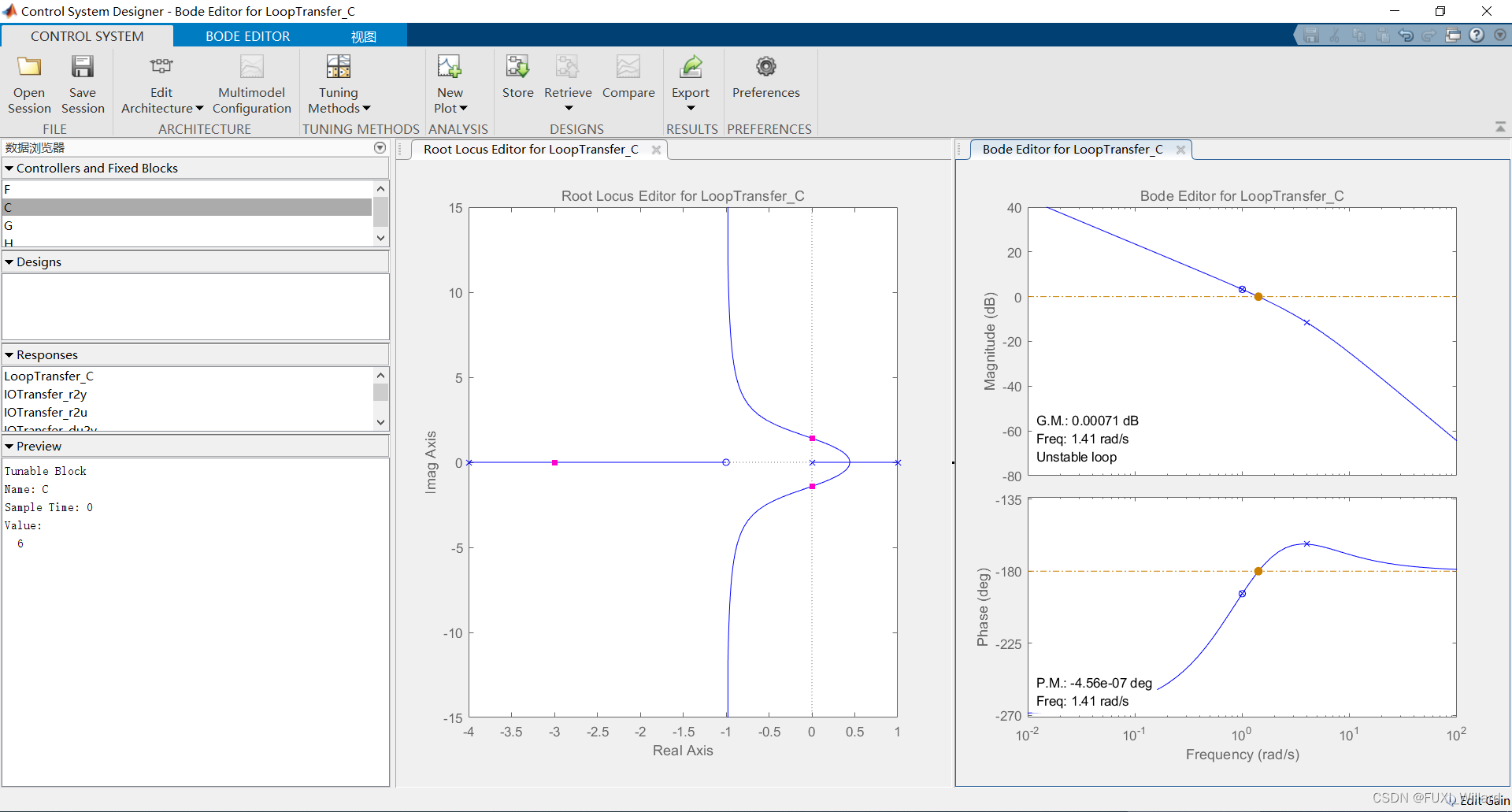

【K=6K=6K=6阶跃响应】

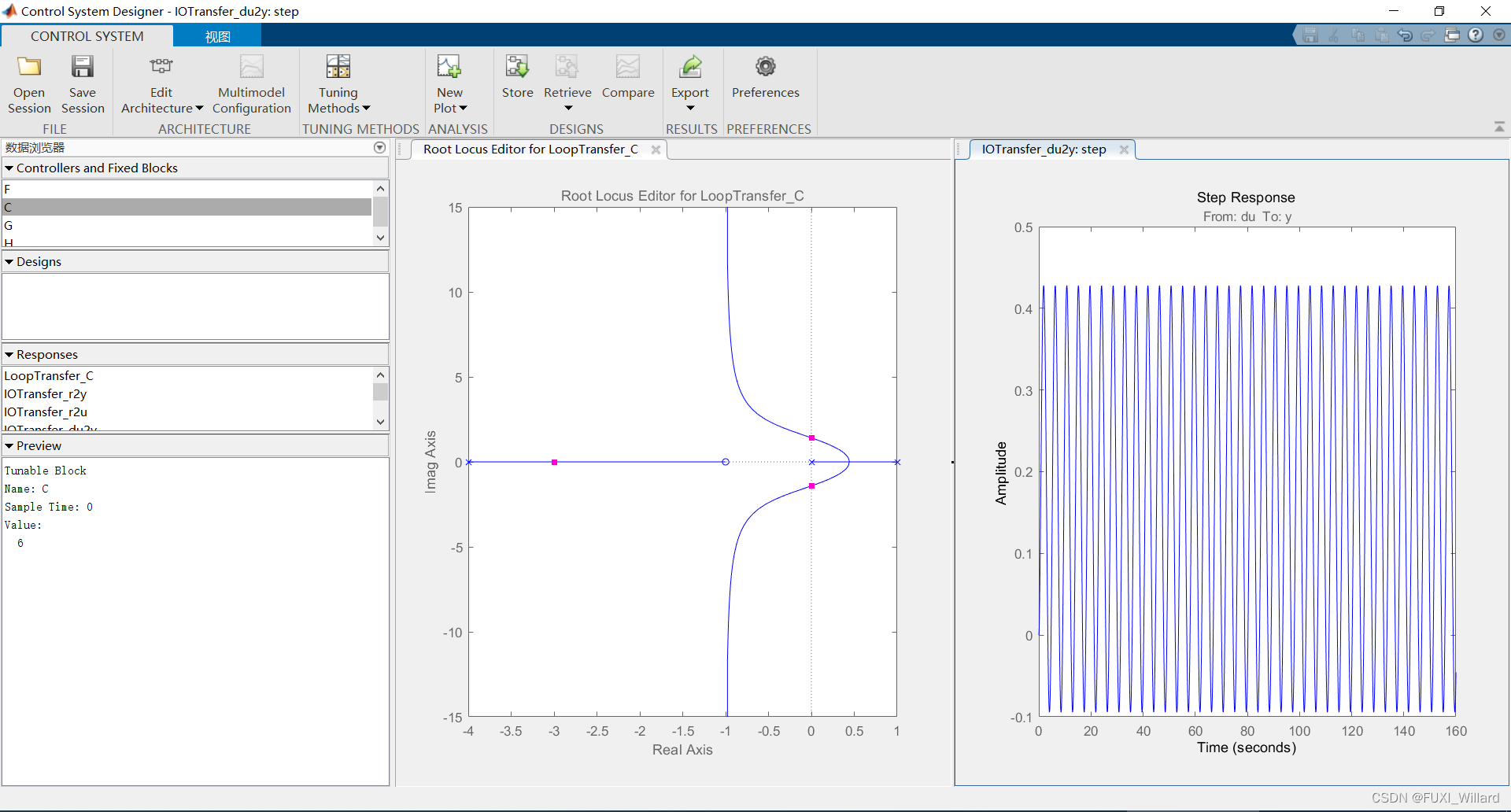
【K=20K=20K=20阶跃响应】