一、从中序与后序遍历序列构造二叉树

题意描述：

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

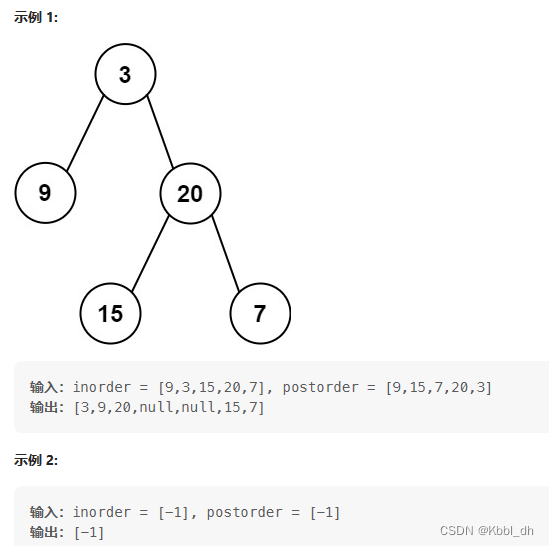
 需要利用后续遍历（左右中）的最后一个元素，即根节点进行对中序遍历数组的切割，之后根据中序遍历的切割结果对后续遍历进行二次切割。

总体来说分为以下步骤：

• 第一步：如果数组大小为零的话，说明是空节点了。

• 第二步：如果不为空，那么取后序数组最后一个元素作为节点元素。

• 第三步：找到后序数组最后一个元素在中序数组的位置，作为切割点

• 第四步：切割中序数组，切成中序左数组和中序右数组 （顺序别搞反了，一定是先切中序数组）

• 第五步：切割后序数组，切成后序左数组和后序右数组

• 第六步：递归处理左区间和右区间

C++完整代码如下所示：

class Solution {
private:TreeNode* traversal(vector& inorder, vector& postorder){if(postorder.size() == 0){return NULL;}// 后序遍历数组最后一个元素，就是当前的中间节点int rootValue = postorder[postorder.size() - 1];TreeNode* node = new TreeNode(rootValue);if(postorder.size() == 1){return node;}int index;for(index = 0; index < inorder.size(); index++){if(inorder[index] == rootValue){break;}}// 切割中序数组// 左闭右开区间：[0, delimiterIndex)vector leftInorder(inorder.begin(), inorder.begin() + index);// [delimiterIndex + 1, end)vector rightInorder(inorder.begin() + index + 1, inorder.end());postorder.resize(postorder.size() - 1);// 切割后序数组// 依然左闭右开，注意这里使用了左中序数组大小作为切割点// [0, leftInorder.size)vector leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());// [leftInorder.size(), end)vector rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());node->left = traversal(leftInorder, leftPostorder);node->right = traversal(rightInorder, rightPostorder);return node;}
public:TreeNode* buildTree(vector& inorder, vector& postorder) {if(inorder.size() == 0 || postorder.size() == 0){return NULL;}return traversal(inorder, postorder);}
};

二、从前序与中序遍历序列构造二叉树

题意描述：

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

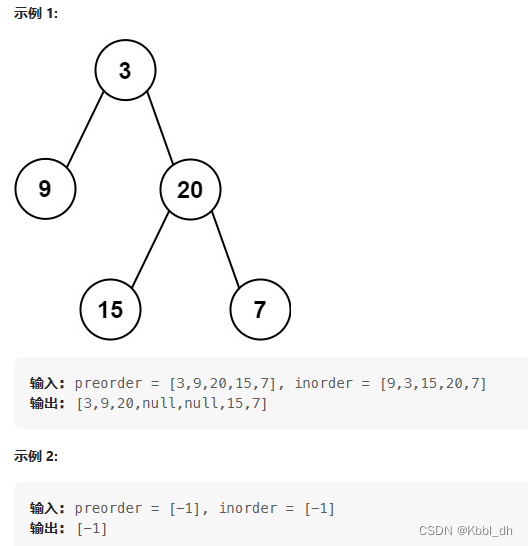
 与从中序与后续遍历序列构造二叉树方法相同。只不过不利用0，而重新定义一个begin和end。

C++完整代码如下：

class Solution {
private:TreeNode* traversal (vector& inorder, int inorderBegin, int inorderEnd, vector& preorder, int preorderBegin, int preorderEnd) {if (preorderBegin == preorderEnd) return NULL;int rootValue = preorder[preorderBegin]; // 注意用preorderBegin 不要用0TreeNode* root = new TreeNode(rootValue);if (preorderEnd - preorderBegin == 1) return root;int delimiterIndex;for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {if (inorder[delimiterIndex] == rootValue) break;}// 切割中序数组// 中序左区间，左闭右开[leftInorderBegin, leftInorderEnd)int leftInorderBegin = inorderBegin;int leftInorderEnd = delimiterIndex;// 中序右区间，左闭右开[rightInorderBegin, rightInorderEnd)int rightInorderBegin = delimiterIndex + 1;int rightInorderEnd = inorderEnd;// 切割前序数组// 前序左区间，左闭右开[leftPreorderBegin, leftPreorderEnd)int leftPreorderBegin =  preorderBegin + 1;int leftPreorderEnd = preorderBegin + 1 + delimiterIndex - inorderBegin; // 终止位置是起始位置加上中序左区间的大小size// 前序右区间, 左闭右开[rightPreorderBegin, rightPreorderEnd)int rightPreorderBegin = preorderBegin + 1 + (delimiterIndex - inorderBegin);int rightPreorderEnd = preorderEnd;root->left = traversal(inorder, leftInorderBegin, leftInorderEnd,  preorder, leftPreorderBegin, leftPreorderEnd);root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, preorder, rightPreorderBegin, rightPreorderEnd);return root;}
public:TreeNode* buildTree(vector& preorder, vector& inorder) {if (inorder.size() == 0 || preorder.size() == 0) return NULL;// 参数坚持左闭右开的原则return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());}
};