还不会拓扑排序?看这一篇就够了
目录
- 一、什么是拓扑排序?
- 二、拓扑排序的实现
- 2.1 拓扑排序模版
- 三、拓扑排序的应用
- 3.1 有向图的拓扑序列
- 3.2 家谱树
- 3.3 奖金
- 3.4 可达性统计
- 3.5 Directing Edges
一、什么是拓扑排序?
拓扑排序是一种有向无环图(DAG)的顶点排序方法,它将一个有向无环图中的所有顶点排成一个线性序列,使得图中任意一条有向边上的起点排在终点的前面。
这样说还不够具体,我们先来看一个例子。假设某大学的课程安排如下:
| 课程编号 | 课程名称 | 先修课程 |
|---|---|---|
| 111 | 高等数学 | −-− |
| 222 | 程序设计基础 | −-− |
| 333 | 离散数学 | 1,21,\,21,2 |
| 444 | 数据结构 | 2,32,\,32,3 |
| 555 | 高级语言程序设计 | 222 |
| 666 | 编译方法 | 4,54,\,54,5 |
| 777 | 操作系统 | 4,94,\,94,9 |
| 888 | 普通物理 | 111 |
| 999 | 计算机原理 | 888 |
为了顺利修完这九门课程,我们必须安排一个合理的学习顺序。
首先根据以上表格构建一个有向图,即若 jjj 的先修课程有 iii,则画一条 iii 到 jjj 的有向边,于是可以得到:
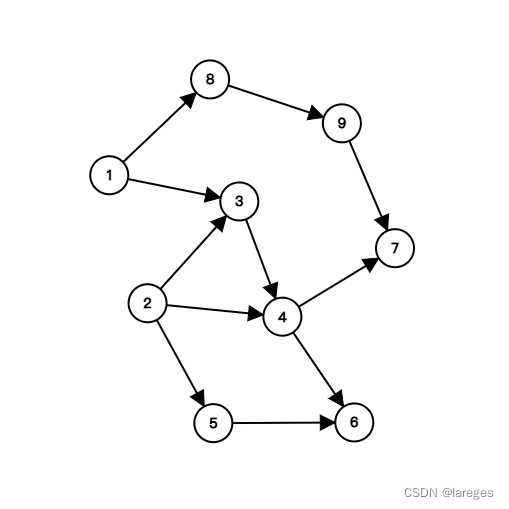
一个合理的学习顺序是:1→8→9→2→3→5→4→7→61\to8\to9\to2\to3\to5\to4\to7\to61→8→9→2→3→5→4→7→6,该序列又称拓扑序列,是对上述有向图进行拓扑排序后的结果。
可以看出,拓扑序列不唯一。例如,1→8→9→2→3→5→4→6→71\to8\to9\to2\to3\to5\to4\to6\to71→8→9→2→3→5→4→6→7 也是满足要求的学习顺序。
此外还可以证明,DAG一定存在拓扑序列,存在拓扑序列的图也一定是DAG,因此DAG又被称为拓扑图。
二、拓扑排序的实现
拓扑排序的具体步骤如下:
- 找到所有入度为 000 的顶点,并将其输出到拓扑序列中。
- 将这些顶点从图中删除,并将所有以该顶点为起点的边的终点的入度减 111。
- 不断重复以上两个操作,直到所有的顶点都被输出到拓扑序列中或者图中不存在入度为 000 的顶点为止。
代码实现:
int n, m; // n表示节点数量,m表示边的数量
int h[N], e[N], ne[N], idx; // 邻接表存图
int in[N]; // 保存每个点的入度
vector L; // 存储拓扑序列// 拓扑排序算法
void topo_sort() {queue q;for (int i = 1; i <= n; i++)// 找到所有入度为0的点然后将其添加到队列中,同时也输出到拓扑序列中if (in[i] == 0) {q.push(i);L.push_back(i);}while (!q.empty()) {auto t = q.front();q.pop();for (int i = h[t]; ~i; i = ne[i]) { // 遍历t的所有相邻节点int j = e[i];in[j]--; // 将相邻节点的入度-1// 如果相邻节点的入度减到0,则入队列,同时将其输出到拓扑序列中if (in[j] == 0) {q.push(j);L.push_back(i);}}}
}
如果 L.size() == n 成立,说明该图存在拓扑序列,否则说明该图不是DAG。
拓扑排序的时间复杂度和BFS相同,均为 O(n+m)O(n+m)O(n+m)。
2.1 拓扑排序模版
上述代码显得过于臃肿,我们可以进一步简化以形成模版(务必背过)。
void topo_sort() {queue q;for (int i = 1; i <= n; i++)if (!in[i]) q.push(i);while (!q.empty()) {auto t = q.front();q.pop();L.push_back(t);for (int i = h[t]; ~i; i = ne[i]) {int j = e[i];if (!--in[j]) q.push(j);}}
}
三、拓扑排序的应用
3.1 有向图的拓扑序列
🔗 原题链接:AcWing 848. 有向图的拓扑序列
直接套模板即可。
#include using namespace std;const int N = 1e5 + 10;int n, m;
int h[N], e[N], ne[N], idx;
int in[N];
vector L;void add(int a, int b) {e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}void topo_sort() {queue q;for (int i = 1; i <= n; i++)if (!in[i]) q.push(i);while (!q.empty()) {auto t = q.front();q.pop();L.push_back(t);for (int i = h[t]; ~i; i = ne[i]) {int j = e[i];if (!--in[j]) q.push(j);}}
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);memset(h, -1, sizeof h);cin >> n >> m;while (m--) {int x, y;cin >> x >> y;add(x, y), in[y]++;}topo_sort();if (L.size() == n) {for (auto i: L) cout << i << ' ';cout << "\n";} else cout << -1 << "\n";return 0;
}
3.2 家谱树
🔗 原题链接:AcWing 1191. 家谱树
如果 bbb 是 aaa 的孩子,则画一条由 aaa 指向 bbb 的有向边,然后拓扑排序即可。
#include using namespace std;const int N = 110, M = N * N / 2;int n;
int h[N], e[M], ne[M], idx;
int in[N];
vector L;void add(int a, int b) {e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}void topo_sort() {queue q;for (int i = 1; i <= n; i++)if (!in[i]) q.push(i);while (!q.empty()) {auto t = q.front();q.pop();L.push_back(t);for (int i = h[t]; ~i; i = ne[i]) {int j = e[i];if (!--in[j]) q.push(j);}}
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);memset(h, -1, sizeof h);cin >> n;for (int i = 1; i <= n; i++) {int x;while (cin >> x, x) {add(i, x);in[x]++;}}topo_sort();for (auto i: L) cout << i << ' ';cout << "\n";return 0;
}
3.3 奖金
🔗 原题链接:AcWing 1192. 奖金
对于建图,如果 bbb 的奖金比 aaa 高,则画一条 aaa 到 bbb 的有向边。
要使总奖金最少,很显然,初始时所有入度为 000 的点的奖金都为 100100100 元。之后,对于图中任意两点 x,yx,yx,y,如果存在 xxx 到 yyy 的有向边,那么 yyy 的奖金应当比 xxx 的奖金多一元。
我们可以让队列不止保存员工的编号,还保存每位员工的奖金,这样在遍历的时候就能够方便的去计算每位员工的奖金了。
#include using namespace std;const int N = 10010, M = 20010;int n, m;
int h[N], e[M], ne[M], idx;
int in[N];
vector L;void add(int a, int b) {e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}void topo_sort() {queue> q;for (int i = 1; i <= n; i++)if (!in[i]) q.emplace(i, 100);while (!q.empty()) {auto [t, bonus] = q.front();q.pop();L.push_back(bonus);for (int i = h[t]; ~i; i = ne[i]) {int j = e[i];if (!--in[j]) q.emplace(j, bonus + 1); // 多一元}}
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);memset(h, -1, sizeof h);cin >> n >> m;while (m--) {int x, y;cin >> x >> y;add(y, x), in[x]++;}topo_sort();if (L.size() == n) cout << accumulate(L.begin(), L.end(), 0) << "\n";else cout << "Poor Xed\n";return 0;
}
3.4 可达性统计
🔗 原题链接:AcWing 164. 可达性统计
本题可以用BFS暴力求解,时间复杂度为 O(n(n+m))≈1.8×109O(n(n+m))\approx1.8\times 10^9O(n(n+m))≈1.8×109,只能过 3/53/53/5 的测试点。
不妨设从 xxx 出发能够到达的点的集合为 f(x)f(x)f(x),易知
f(x)={x}∪⋃y∈N(x)f(y)f(x)=\{x\}\cup \bigcup_{y\in N(x)} f(y) f(x)={x}∪y∈N(x)⋃f(y)
也就是说,从 xxx 出发能够到达的点的集合为从「xxx 的各个后继节点」出发能够到达的点的集合的并集再加上 xxx 自身。所以,只有在计算出一个点的所有后继节点的 fff 值之后,我们才能够算出该点的 fff 值。这启发我们先对图进行拓扑排序得到一个拓扑序列,然后再倒序计算。
我们可以用 nnn 位二进制数来存储每个 f(x)f(x)f(x),其中第 iii 位是 111 表示 xxx 能到 iii,第 iii 位是 000 表示 xxx 不能到 iii。这样一来,对若干个集合求并就相当于对若干个二进制数进行按位或运算,每个 f(x)f(x)f(x) 中 111 的个数就代表了从 xxx 出发能够到达的节点的数量。
#include using namespace std;const int N = 30010;int n, m;
int h[N], e[N], ne[N], idx;
int in[N];vector L;
bitset f[N];void add(int a, int b) {e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}void topo_sort() {queue q;for (int i = 1; i <= n; i++)if (!in[i]) q.push(i);while (!q.empty()) {auto t = q.front();q.pop();L.push_back(t);for (int i = h[t]; ~i; i = ne[i]) {int j = e[i];if (!--in[j]) q.push(j);}}
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);memset(h, -1, sizeof h);cin >> n >> m;while (m--) {int x, y;cin >> x >> y;add(x, y), in[y]++;}topo_sort();for (int i = n - 1; ~i; i--) { // 倒序遍历int j = L[i];f[j][j] = 1; // j一定能到达自身for (int k = h[j]; ~k; k = ne[k])f[j] |= f[e[k]]; // 按照公式计算出f[j]的值}for (int i = 1; i <= n; i++) cout << f[i].count() << "\n";return 0;
}
3.5 Directing Edges
🔗 原题链接:CF 1385E
本题说白了就是给图中的所有无向边指定方向,使得最终得到的图是一个DAG。
我们可以先考虑仅由有向边构成的子图,如果这个子图都不是DAG,那么后续无论怎样为无向边指定方向(相当于添加有向边)都不可能构成DAG,此时应当输出 NO。如果这个子图是DAG,那么我们一定可以通过指定无向边的方向来构造出新的DAG。
具体来说,我们先对有向边构成的子图进行拓扑排序,于是可以得到一个拓扑序列。对于每一个无向边 (a,b)(a,b)(a,b),若 aaa 在拓扑序列中的下标小于 bbb 在拓扑序列中的下标,则添加有向边 a→ba\to ba→b,否则添加有向边 b→ab\to ab→a,这样可以保证添加完有向边后得到的图仍然是DAG。
#include using namespace std;const int N = 2e5 + 10;int n, m;
int h[N], e[N], ne[N], idx;
int in[N];void add(int a, int b) {e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}void topo_sort(vector &L) {queue q;for (int i = 1; i <= n; i++)if (!in[i]) q.push(i);while (!q.empty()) {auto t = q.front();q.pop();L.push_back(t);for (int i = h[t]; ~i; i = ne[i]) {int j = e[i];if (!--in[j]) q.push(j);}}
}void solve() {memset(h, -1, sizeof h);memset(in, 0, sizeof in);vector L;vector> edges;cin >> n >> m;while (m--) {int t, x, y;cin >> t >> x >> y;if (t) add(x, y), in[y]++;else edges.emplace_back(x, y);}topo_sort(L);if (L.size() != n) cout << "NO\n";else {cout << "YES\n";// 先输出有向图部分for (int i = 1; i <= n; i++)for (int j = h[i]; ~j; j = ne[j])cout << i << ' ' << e[j] << "\n";vector pos(n + 1); // 因为节点的编号是从1开始的,所以要多开一个for (int i = 0; i < n; i++) pos[L[i]] = i;// 再输出补全的部分for (auto [a, b]: edges) {if (pos[a] > pos[b]) swap(a, b);cout << a << ' ' << b << "\n";}}
}int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int t;cin >> t;while (t--) {solve();}return 0;
}
上一篇:【Linux】用户和权限
下一篇:宽字节注入