算法练习-二叉树

文章目录

• 算法练习-二叉树
• • 1 二叉树的基础知识
  • • 1.1 二叉树的存储
    • • 1.1.1 基于指针的存储方式
      • 1.1.2基于数组的存储方式
    • 1.2 二叉树的遍历
    • • 1.2.1 前序遍历
      • 1.2.2 中序遍历
      • 1.2.3 后序遍历
    • 1.3 二叉查找树
    • • 1.3.1 二叉查找树的实现
      • 1.3.2 二叉查找树的插入
      • 1.3.3 二叉查找树的删除操作
  • 2 二叉树相关题型
  • • 2.1 二叉树前中后序遍历
    • • 2.1.1 N叉树的前序遍历
      • 2.1.2 N叉树的后序遍历
    • 2.2 二叉树按层遍历
    • • 2.2.1 从上到下打印二叉树
    • 2.3 二叉树上的递归
    • • 2.3.1 二叉树的最大深度
      • 2.3.2 平衡二叉树
    • 2.4 二叉查找树
    • • 2.4.1 二叉搜索树的第k大节点

1 二叉树的基础知识

1.1 二叉树的存储

1.1.1 基于指针的存储方式

public class BinartTree {public class Node { // 节点的定义public int data;public Node left;public Node right;}private Node root = null;
}

1.1.2基于数组的存储方式

用数组来存储所有的节点。根节点存储在下标为1的位置

节点之间的父子关系，通过数组下表计算得到：如果节点x的下标是i

——下标为 i*2 的位置存储左子节点

——下标为 2*i+1 的位置存储右子节点

——下标为 i / 2 的位置存储就是父节点

这种存储方式基本只适用于完全二叉树，因为非完全二叉树会产生很多的空洞。

1.2 二叉树的遍历

1.2.1 前序遍历

先打印根节点，然后再先序遍历左子树，最后先序遍历右子树

public void preOrder(Node root) {if (root == null) return;System.out.println(root.data);preOrder(root.left);preOrder(root.right);
}

1.2.2 中序遍历

先中序遍历左子树，再打印根节点，最后中序遍历右子树

public void inOrder(Node root) {if (root == null) return;inOrder(root.left);System.out.println(root.data);inOrder(root.right);
}

1.2.3 后序遍历

先后序遍历左子树，再后序遍历右子树，最后打印根节点

public void postOrder(Node root) {if (root == null) return;postOrder(root.left);postOrder(root.right);System.out.println(root.data);
}

1.3 二叉查找树

二叉查找树是一种特殊的二叉树，支持快速查找、插入、删除数据

对于二叉查找树中任意一个节点，其左子树中每个节点的值，都小于这个节点的值。其右子树每个节点的值，都大于这个节点的值

1.3.1 二叉查找树的实现

• 递归实现

public class Node {private int data;private Node left;private Node right;public Node(int data) {this.data = data;}
}private Node root = null;public Node find_r(Node root, int data) {if (root == null) return null;if (root.data == data) return root;if (data < root.data) {return find_r(root.left, data);} else {return find_r(root.right, data);}
}

• 非递归实现

public Node find(Node root, int data) {Node p = root;while (p != null) {if (data < p.data) {p = p.left;} else if (data > p.data) {p = p.right;} else {return p;}}return null;
}

1.3.2 二叉查找树的插入

如果要插入的数比当前节点的值小，且当前节点的左子树为空，则将新数据插入到左子节点的位置，如果左子树不为空，再递归遍历左子树，找到插入位置

如果要插入的数比当前节点的值大，且当前节点的右子树为空，则将新数据插入到右子节点的位置，如果右子树不为空，再递归遍历右子树，找到插入位置

• 递归实现

if (root == null) {root = new Node(data);return;
}public void insert_r(Node root, int data) {if (data > root.data) {if (root.right == null) {root.right = new Node(data);} else {insert_r(root.right, data);}} else {if (root.left == null) {root.left = new Node(data);} else {insert_r(root.left, data);}}
}

• 非递归实现

public void insert(int data) {if (root == null) {root = new Node(data);return;}Node p = root;while(p != null) {if(data > p.data) {if (p.right == null) {p.right = new Node(data);return;}p = p.right;} else {if (p.left == null) {p.left = new Node(data);return;}p = p.left;}}
}

1.3.3 二叉查找树的删除操作

针对待删除的节点的子节点的个数不同，分三种情况处理

1. 要删除的节点没有子节点。直接将父节点中指向要删除的节点的指针设置为null即可
2. 要删除的节点只有一个子节点。更新父节点中指向要删除的节点的指针，让他重新指向要删除节点的子节点
3. 要删除的节点有两个子节点。需要找到这个节点的右子树中的最小节点，把他替换到要删除的节点上(或者左子树的最大节点，总之是最接近这个被删除节点值的节点)。然后再删除掉这个最小节点，因为最小节点肯定没有左子节点，然后用上面两条规则删除这个最小节点

public void delete(int data) {Node p = root; // p指向要删除的节点，初始化指向根节点Node pp = null; // pp指向的是p的父节点while(p != null && p.data != data) { // 查找要删除的节点及其父节点pp = p;if (data > p.data) p = p.right;else p = p.left;}if (p == null) return; // 没找到// 要删除的节点有两个子节点if(p.left != null && p.right != null) { // 查找右子树的最小节点Node minP = p.right;Node minPP = p; // minPP表示minP的父节点while (minP.left != null) {minPP = minP;minP = minP.left;}p.data = minP.data;p = minP;pp = minPP;}// 删除节点是叶子节点或者只有一个子节点Node child = null;if (p.left != null) child = p.left;else if (p.right != null) child = p.right;if (pp == null) root = child; // 删除的是根节点else if (pp.left == p) pp.left = child;else pp.right = child;
}

2 二叉树相关题型

2.1 二叉树前中后序遍历

2.1.1 N叉树的前序遍历

链接：https://leetcode.cn/problems/n-ary-tree-preorder-traversal

给定一个 n 叉树的根节点 root ，返回 其节点值的 前序遍历 。

n 叉树 在输入中按层序遍历进行序列化表示，每组子节点由空值 null 分隔（请参见示例）。

示例 1：

输入：root = [1,null,3,2,4,null,5,6]
输出：[1,3,5,6,2,4]
示例 2：

输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[1,2,3,6,7,11,14,4,8,12,5,9,13,10]

提示：

节点总数在范围 [0, 104]内
0 <= Node.val <= 104
n 叉树的高度小于或等于 1000

进阶：递归法很简单，你可以使用迭代法完成此题吗?

/*
// Definition for a Node.
class Node {public int val;public List children;public Node() {}public Node(int _val) {val = _val;}public Node(int _val, List _children) {val = _val;children = _children;}
};
*/class Solution {List result = new ArrayList<>();public List preorder(Node root) {preorder_r(root);return result;}public void preorder_r(Node root) {if (root == null) return;result.add(root.val);for (int i = 0; i < root.children.size(); i++) {preorder_r(root.children.get(i));}}
}

2.1.2 N叉树的后序遍历

链接：https://leetcode.cn/problems/n-ary-tree-postorder-traversal

给定一个 n 叉树的根节点 root ，返回 其节点值的 后序遍历 。

n 叉树 在输入中按层序遍历进行序列化表示，每组子节点由空值 null 分隔（请参见示例）。

示例 1：

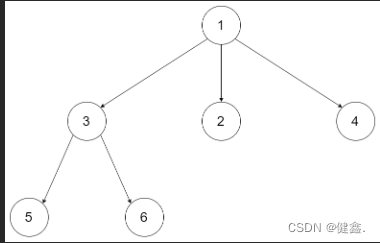
输入：root = [1,null,3,2,4,null,5,6]
输出：[5,6,3,2,4,1]
示例 2：

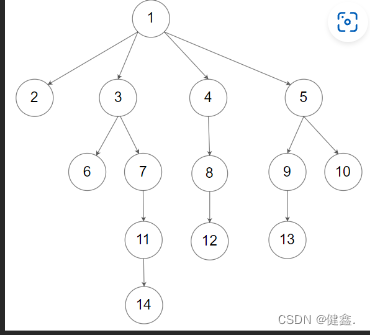
输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[2,6,14,11,7,3,12,8,4,13,9,10,5,1]

提示：

节点总数在范围 [0, 104] 内
0 <= Node.val <= 104
n 叉树的高度小于或等于 1000

进阶：递归法很简单，你可以使用迭代法完成此题吗?

/*
// Definition for a Node.
class Node {public int val;public List children;public Node() {}public Node(int _val) {val = _val;}public Node(int _val, List _children) {val = _val;children = _children;}
};
*/class Solution {List result = new ArrayList<>();public List postorder(Node root) {postorder_r(root);return result;}public void postorder_r(Node root) {if (root == null) return;for (int i = 0; i < root.children.size(); i++) {postorder_r(root.children.get(i));}result.add(root.val);}
}

2.2 二叉树按层遍历

2.2.1 从上到下打印二叉树

链接：https://leetcode.cn/problems/cong-shang-dao-xia-da-yin-er-cha-shu-lcof

从上到下打印出二叉树的每个节点，同一层的节点按照从左到右的顺序打印。

例如:
给定二叉树: [3,9,20,null,null,15,7],

    3/ \9  20/  \15   7

返回：

[3,9,20,15,7]

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode(int x) { val = x; }* }*/
class Solution {public int[] levelOrder(TreeNode root) {if (root == null) return new int[0];List result = new ArrayList<>();Queue queue = new LinkedList<>();queue.add(root);while (!queue.isEmpty()) {TreeNode node = queue.poll();result.add(node.val);if (node.left != null) {queue.add(node.left);}if (node.right != null) {queue.add(node.right);}}int[] resultArray = new int[result.size()];for (int i = 0; i < result.size(); i++) {resultArray[i] = result.get(i);}return resultArray;}
}

2.3 二叉树上的递归

2.3.1 二叉树的最大深度

链接：https://leetcode.cn/problems/maximum-depth-of-binary-tree

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，

    3/ \9  20/  \15   7

返回它的最大深度 3 。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public int maxDepth(TreeNode root) {if (root == null) {return 0;}return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;}
}

2.3.2 平衡二叉树

链接：https://leetcode.cn/problems/ping-heng-er-cha-shu-lcof

输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左右子树的深度相差不超过1，那么它就是一棵平衡二叉树。

示例 1:

给定二叉树 [3,9,20,null,null,15,7]

    3/ \9  20/  \15   7

返回 true 。

示例 2:

给定二叉树 [1,2,2,3,3,null,null,4,4]

       1/ \2   2/ \3   3/ \4   4

返回 false 。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode(int x) { val = x; }* }*/
class Solution {private boolean balanced = true;public boolean isBalanced(TreeNode root) {height(root);return balanced;}private int height(TreeNode root) {if (root == null) return 0;if (balanced == false) return 0;int leftHeight = height(root.left);int rightHeight = height(root.right);if (Math.abs(leftHeight - rightHeight) > 1) {balanced = false;}return Math.max(leftHeight, rightHeight) + 1;}
}

2.4 二叉查找树

2.4.1 二叉搜索树的第k大节点

链接：https://leetcode.cn/problems/er-cha-sou-suo-shu-de-di-kda-jie-dian-lcof

给定一棵二叉搜索树，请找出其中第 k 大的节点的值。

示例 1:

输入: root = [3,1,4,null,2], k = 1
3
/
1 4

2
输出: 4
示例 2:

输入: root = [5,3,6,2,4,null,null,1], k = 3
5
/
3 6
/
2 4
/
1
输出: 4

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode(int x) { val = x; }* }*/
class Solution {int count = 0;int result;public int kthLargest(TreeNode root, int k) {inorder(root, k);return result;}private void inorder(TreeNode root, int k) {if (count >= k) return;if (root == null) return;inorder(root.right, k);count++;if (count == k) {result = root.val;return;}inorder(root.left, k);}
}