1.汉明距离

两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。

给你两个整数 x 和 y，计算并返回它们之间的汉明距离。

示例 1：

输入：x = 1, y = 4
输出：2
解释：
1   (0 0 0 1)
4   (0 1 0 0)↑   ↑
上面的箭头指出了对应二进制位不同的位置。

示例 2：

输入：x = 3, y = 1
输出：1

我的解法（异或运算性质）

class Solution {public int hammingDistance(int x, int y) {// Integer.bitCount()返回指定int值的2的补位二进制表示中的1位数。return Integer.bitCount(x ^ y);}
}

总结，异或运算的三个性质：

1. 任何数和0做异或运算，结果仍是原来的数；
2. 任何数和自身做异或运算，结果为0；
3. 异或运算符合交换律。

2. 二叉树的直径

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。

示例 :
给定二叉树

1/ \2   3/ \     4   5    

返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。

我的解法（递归）

class Solution {int res;public int diameterOfBinaryTree(TreeNode root) {res = -1; depth(root);return res - 1;}public int depth(TreeNode root){if(root == null){return 0;}int left = depth(root.left);int right = depth(root.right);res = Math.max(res, left + right + 1);return Math.max(left, right) + 1;}
}

3.括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

输入：n = 3
输出：["((()))","(()())","(())()","()(())","()()()"]

示例 2：

输入：n = 1
输出：["()"]

我的解法（dfs、递归）

class Solution {public List generateParenthesis(int n) {List res = new ArrayList<>();dfs("", n, n, res);return res;}/*** curStr: 当前递归得到的结果* left: 左括号剩余个数* right: 右括号剩余个数* res: 结果集*/public void dfs(String curStr, int left, int right, List res){if(left == 0 && right == 0){//左右括号个数都为0 递归结束 将最终结果添加到结果集res.add(curStr);return;}if(left > right){// 左括号剩余个数大于右括号剩余个数 剪枝// 例如 ()) 这种情况显然是不允许的return ;}if(left > 0){// 左括号大于 0 即可产生分支// 例如 ( (( 只要左括号个数大于零递归就可以继续dfs(curStr + "(" , left - 1, right, res);}// 右括号剩余数量 > 左括号剩余数量 才可产生分支// 假设 n = 2// ( : 此时 left = 1, right = 2 显然可以// (): 此时 left = 1, right = 1 显然不可以 如果可以就成了这样 ())if(right > left){dfs(curStr + ")", left, right - 1, res);}}
}

4.二叉树的层序遍历

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

示例 1：

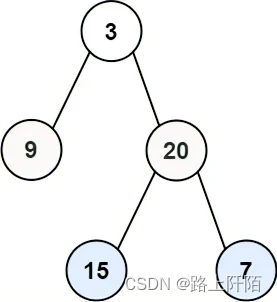
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

我的解法（bfs）

class Solution {public List> levelOrder(TreeNode root) {List> res = new ArrayList<>();// 辅助队列 先进先出Queue queue = new ArrayDeque<>();if(root == null) return res;queue.add(root);while(!queue.isEmpty()){// 记录每一层的个数int n = queue.size();// 保存每一层的节点List list = new ArrayList<>();for(int i = 0; i < n; ++i){TreeNode node = queue.poll();list.add(node.val);if(node.left != null){queue.add(node.left);}if(node.right != null){queue.add(node.right);}}// 将每一层的节点都加入返回集合中res.add(list);}return res;}
}

地图分析

你现在手里有一份大小为 n x n 的 网格 grid，上面的每个 单元格 都用 0 和 1 标记好了。其中 0 代表海洋，1 代表陆地。

请你找出一个海洋单元格，这个海洋单元格到离它最近的陆地单元格的距离是最大的，并返回该距离。如果网格上只有陆地或者海洋，请返回 -1。

我们这里说的距离是「曼哈顿距离」（ Manhattan Distance）：(x0, y0) 和 (x1, y1) 这两个单元格之间的距离是 |x0 - x1| + |y0 - y1| 。

输入：grid = [[1,0,1],[0,0,0],[1,0,1]]
输出：2
解释： 
海洋单元格 (1, 1) 和所有陆地单元格之间的距离都达到最大，最大距离为 2。

我的解法（bfs）

class Solution {public int maxDistance(int[][] grid) {int N = grid.length;Queue queue = new ArrayDeque<>();// 将所有陆地节点加入队列for(int i = 0; i < N; ++i){for(int j = 0; j < N; j++){if(grid[i][j] == 1){queue.add(new int[]{i,j});}}}// 如果网格上只有陆地或者海洋，返回 -1。if(queue.isEmpty() || queue.size() == N * N) return -1;// 每一个陆地节点相邻的四个节点// (a,b) => (a - 1, b) (a + 1, b) (a, b - 1) (a, b + 1)int[][] moves = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};// 记录遍历层数int res = -1; while(!queue.isEmpty()){res++;int n = queue.size();for(int i = 0; i < n; ++i){int[] arr = queue.poll();int r = arr[0];int c = arr[1];for(int[] move : moves){int r2 = r + move[0];int c2 = c + move[1];if(isInArea(N, r2, c2) && grid[r2][c2] == 0){grid[r2][c2] = 2;queue.add(new int[]{r2, c2});}} }}return res;}// 判断坐标 (r, c) 是否在网格中public boolean isInArea(int n, int r, int c){return 0 <= r && r < n && 0 <= c && c < n;}
}