红黑树

概念

红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出2倍，因而是接近平衡的（不是严格平衡）。

性质

性质3、4最为重要，性质5可以忽略不看

1. 每个结点不是红色就是黑色。
2. 根节点是黑色的。
3. 没有连续的红色节点，如果一个节点是红色的，则它的两个孩子结点是黑色的。但是一个节点是黑色的，它的孩子可以是黑色的。
4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点。
5. 每个NIL节点/叶子节点/空节点都是黑色的，此处的叶子结点==空结点==NIL节点。

满足上面的性质，红黑树就能保证：其最长路径中节点个数不会超过最短路径节点个数的两倍。

最短路径：极端情况下是全黑这条路径，或者一条路经黑色节点的数量。

最长路径：一黑一红相间的路径。

讨论一下红黑树接近平衡的这个概念点

最差的情况：左右极其不平衡的情况是最差的，即一棵子树是黑红相间2log2N2log_2N2log2​N，另一棵子树是全黑log2Nlog_2Nlog2​N。

最优的情况：左右均衡的情况是最好的，即当为全黑 或者 每条路径都是黑红相间且这棵树接近满二叉树的情况。

代码实现

节点定义

在节点的定义中，节点的默认颜色为红色。

原因：若每次新增节点为黑色，那必定违反规则4（所有路径上黑色节点数量相同的这条规则）；而每次新增节点为红色，该节点的父节点不一定是红色的，有可能是黑色的，所以有可能违反规则3（无连续红色节点），故默认颜色为红色。

enum Color { RED, BLACK };template
struct RBTreeNode
{RBTreeNode(const pair& kv, Color color = RED): _kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _color(color){}RBTreeNode* _left;  // 节点的左孩子RBTreeNode* _right; // 节点的右孩子RBTreeNode* _parent;// 节点的双亲KV _kv;				// 节点的值Color _color;		// 节点的默认颜色给成红色的
};

插入

按照二叉搜索的树方式插入新节点，检测新节点插入后，红黑树的性质是否造到破坏，若满足规则直接退出，否则需要更新节点颜色，对红黑树进行旋转着色处理，以满足红黑树的规则。

约定:cur为当前节点，p为父节点，g为祖父节点，u为叔叔节点

//父节点
parent = cur->_parent;
//祖父节点
grandparent = parent->_parent;
//叔叔节点
if(grandparent->left == parent)uncle = grandparent->right;
elseuncle = grandparent->left;

变色的3种情况

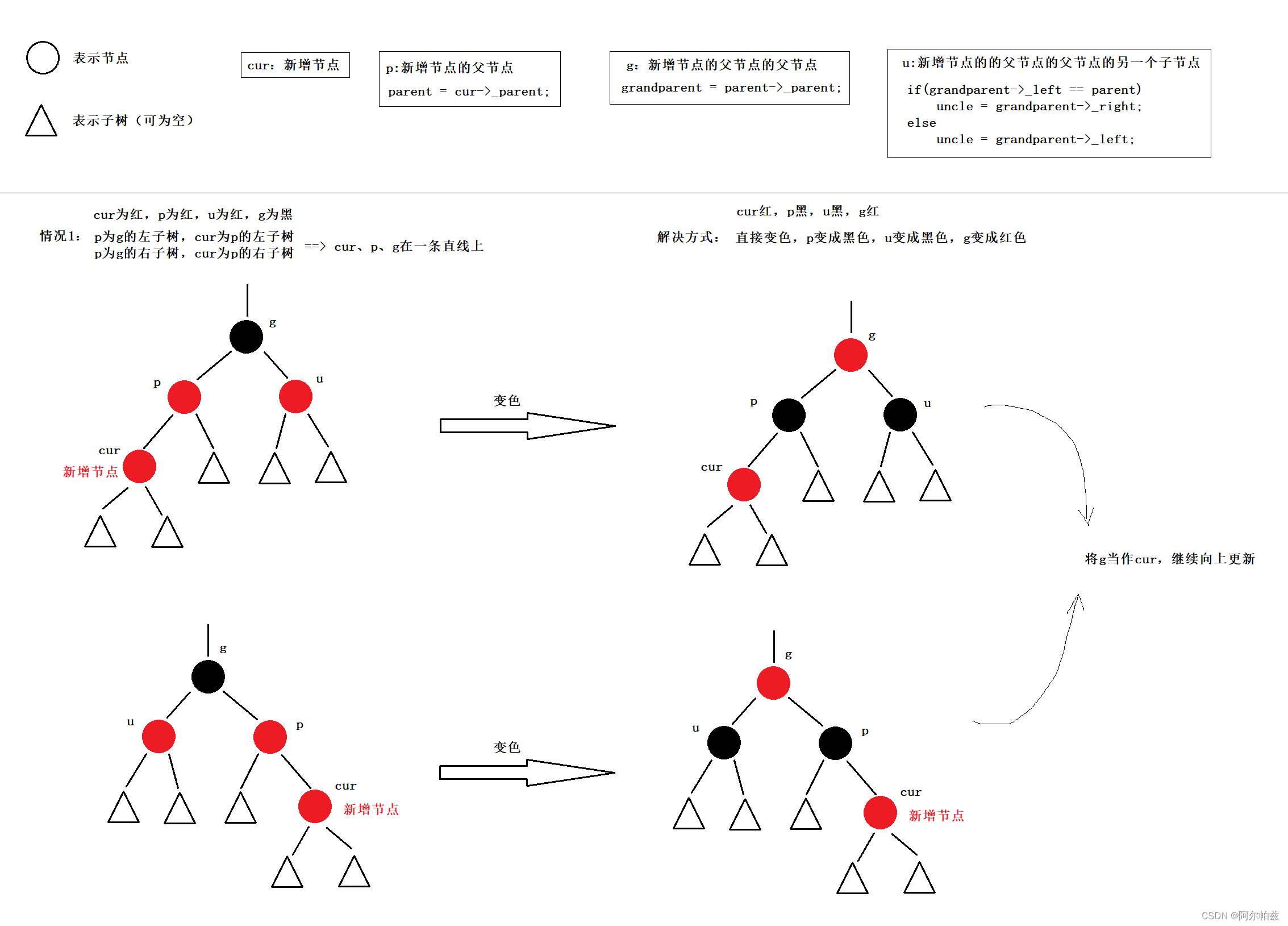
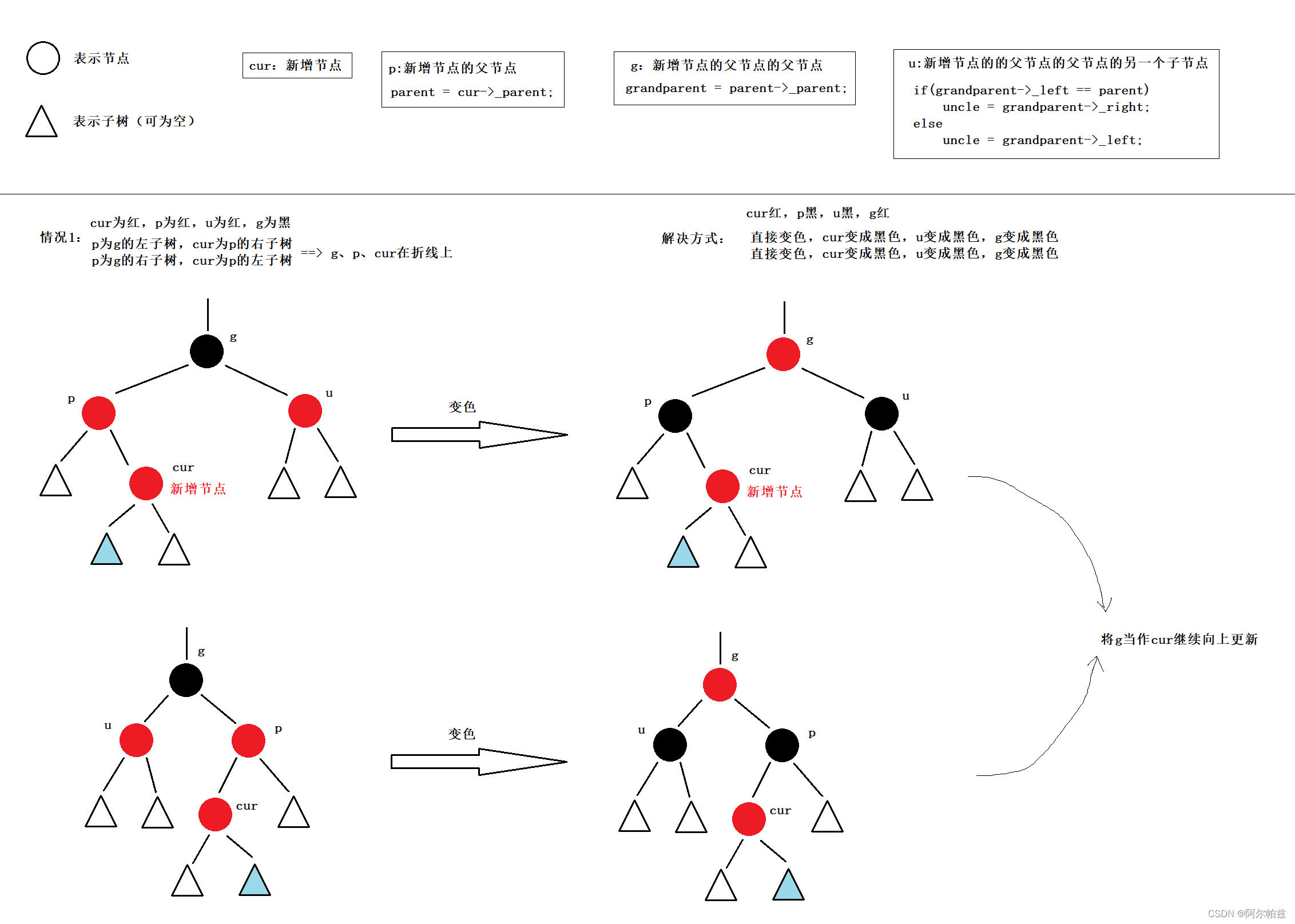
情况1: p为红，g为黑，cur为红，u存在且为红。【p为红，g为黑，cur为红==>while循环判断parent存在且parent颜色为红色即可。首先，parent为红色，则说明grandparent一定存在且为黑色（规则2+规则3）；其次，我们默认新增节点的颜色为红色】

解决方式：

• 将p、u改为黑，g改为红。
• 然后更新g和cur，把原g给cur，cur的父亲给g，继续向上调整。

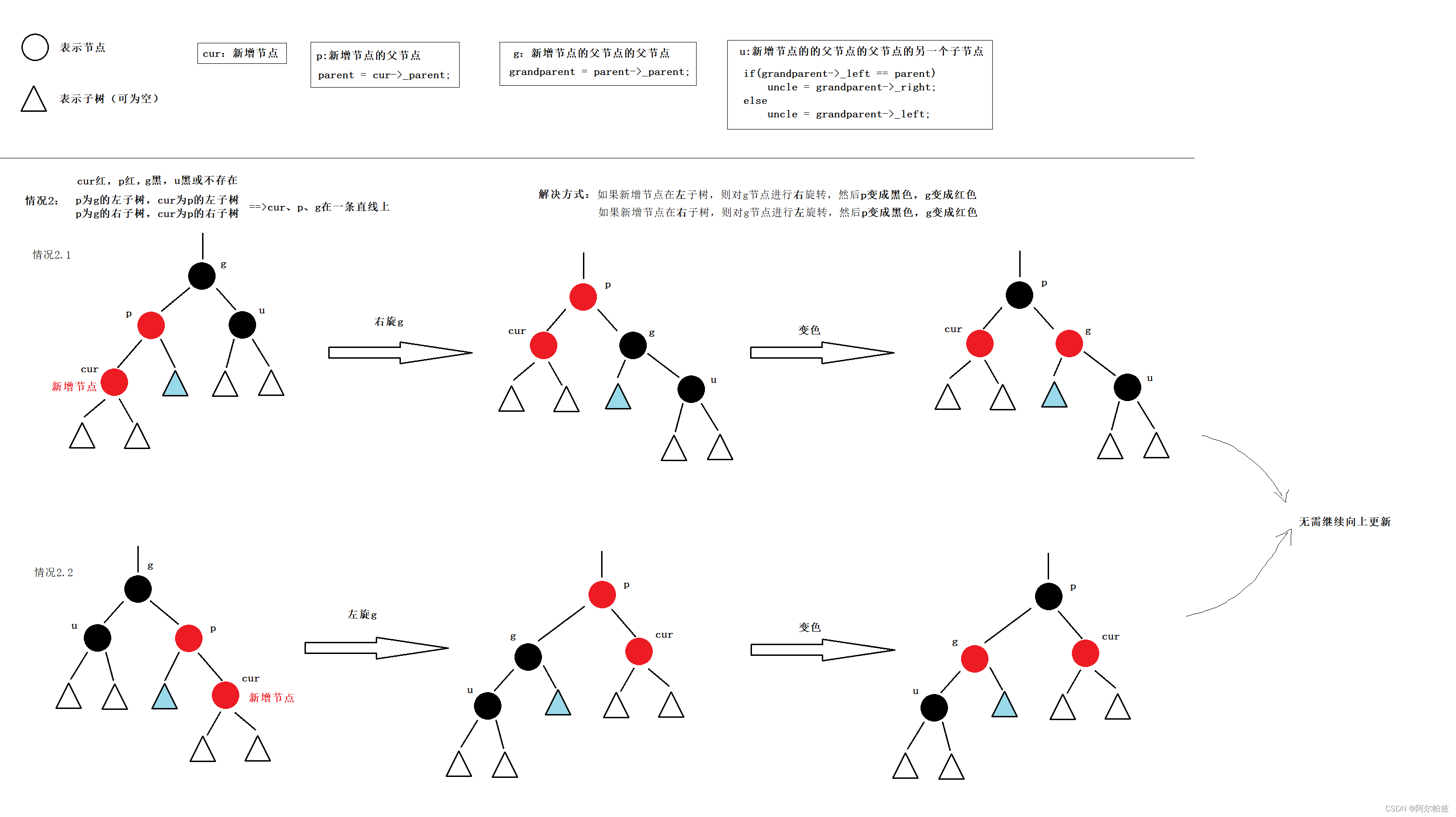
情况2: cur、p、g在一条直线上（2.1 p为g的左孩子，cur为p的左孩子 或者 2.2 p为g的右孩子，cur为p的右孩子），p为红，g为黑，cur为红，u不存在或者u存在且为黑。【p为红，g为黑，cur为红==>while循环判断parent存在且parent颜色为红色即可。首先，parent为红色，则说明grandparent一定存在且为黑色（规则2+规则3）；其次，我们默认新增节点的颜色为红色。u不存在或者u存在且为黑==>在while循环内部进行判断】

解决方式：

• 2.1 p为g的左孩子，cur为p的左孩子，则对g节点进行右单旋转，接着p变成黑色，g变成红色；
• 2.2 p为g的右孩子，cur为p的右孩子，则对g节点进行左单旋转，接着p变成黑色，g变成红色。
• 然后更新g和cur，把原g给cur，cur的父亲给g，继续向上调整。

情况3: cur、p、g在折线上（3.1 p为g的右孩子，cur为p的左孩子 或者 3.2 p为g的左孩子，cur为p的右孩子）， p为红，g为黑，cur为红，u不存在或者u存在且为黑。【p为红，g为黑，cur为红==>while循环判断parent存在且parent颜色为红色即可。首先，parent为红色，则说明grandparent一定存在且为黑色（规则2+规则3）；其次，我们默认新增节点的颜色为红色。u不存在或者u存在且为黑==>在while循环内部进行判断】

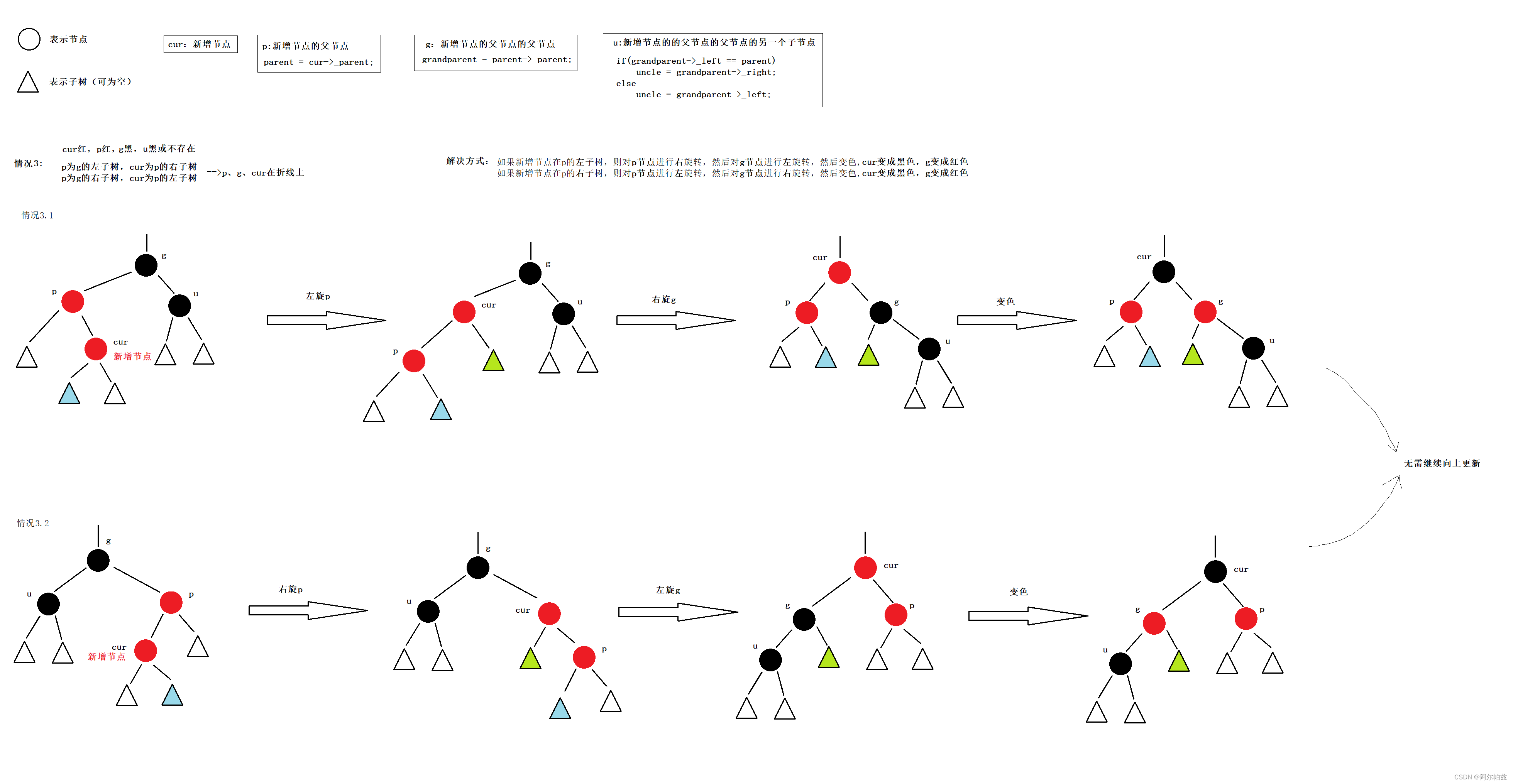
解决方式：

• 3.1 p为g的左孩子，cur为p的右孩子，则对p节点进行左单旋转，接着对g节点进行右单旋转，cur变成黑色，g变成红色。
• 3.2 p为g的右孩子，cur为p的左孩子，则对p节点进行右单旋转，接着对g节点进行左单旋转，cur变成黑色，g变成红色。
• 然后更新g和cur，把原g给cur，cur的父亲给g，继续向上调整。

bool Insert(const std::pair& kv){if (_root == nullptr){_root = new Node(kv);_root->_color = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;// 1、找到合适的插入点while (cur){//要插入的值比当前值大，就访问右子树if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}//要插入的值比当前值小，就访问左子树else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{//不允许数据冗余return false;}}// 2、开始插入以及更新节点颜色cur = new Node(kv);cur->_color = RED;//新插入的节点给红色//比父节点的值大，就插在右边if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}//比父节点的值小，就插在左边else{parent->_left = cur;cur->_parent = parent;}// 3、插入成功，更新节点颜色// 3.1 若父亲颜色为黑色，结束退出	// 3.2 若父亲颜色为红色，开始调整颜色while(parent && RED == parent->_color)//这个循环条件保证了grandparent一定存在，因为parent是红色，而根节点必须为黑色// 因为parent存在，且不是黑色节点，则parent一定不是根，则其一定有双亲{Node* grandparent = parent->_parent;//情况1和x.1if (grandparent->_left == parent){Node* uncle = grandparent->_right;// 情况1: p为红，g为黑，cur为红，u存在且为红if (uncle && uncle->_color == RED){//将p、u改为黑，g改为红parent->_color = BLACK;uncle->_color = BLACK;grandparent->_color = RED;//更新cur节点cur = grandparent;parent = cur->_parent;}//情况2、情况3else{//情况2.1if (cur == parent->_left){RotateR(grandparent);parent->_color = BLACK;grandparent->_color = RED;}//情况3.1else{RotateL(parent);RotateR(grandparent);cur->_color = BLACK;grandparent->_color = RED;}break;}}情况1和x.2else{Node* uncle = grandparent->_left;// 情况1: p为红，g为黑，cur为红，u存在且为红if (uncle && uncle->_color == RED){//将p、u改为黑，g改为红parent->_color = BLACK;uncle->_color = BLACK;grandparent->_color = RED;//更新cur节点cur = grandparent;parent = cur->_parent;}//情况2、情况3else{//情况2.2if (cur == parent->_right){RotateL(grandparent);parent->_color = BLACK;grandparent->_color = RED;}//情况3.2else{RotateR(parent);RotateL(grandparent);cur->_color = BLACK;grandparent->_color = RED;}break;}}			}_root->_color = BLACK;//在修改grandparent的颜色时，有可能改掉了根的颜色，再循环外要改为黑色return true;}

性能

单从时间复杂度来说，AVL树优于红黑树的。但是AVL树通过旋转来调节平衡是有极大的性能消耗，而红黑树不要求严格平衡，减少了旋转带来的性能消耗。