题目描述： 

有 n 个物品和一个大小为 m 的背包. 给定数组 A 表示每个物品的大小和数组 V 表示每个物品的价值.问最多能装入背包的总价值是多大?

1. A[i], V[i], n, m 均为整数
2. 你不能将物品进行切分
3. 你所挑选的要装入背包的物品的总大小不能超过 m
4. 每个物品只能取一次
5. m <= 1000m<=1000\

len(A),len(V)<=100len(A),len(V)<=100

思路分析：

对于每一个物品，它有四种情况：

①价值大，体积大。②价值大，体积小。③价值小，体积大。④价值小，体积小。

因此，在一个背包中，在装入物品的时候，我们需要考虑一种特殊情况和两种常见情况。

特殊情况：装不下。常见情况：放和不放。

我们先定义问题需要的状态：

F(i,j):表示从第i个商品中选择了商品后，大小为j的背包的价值。

状态转移方程：

图中，F中的i是从1开始的，A和V中的i和j是从0开始的。

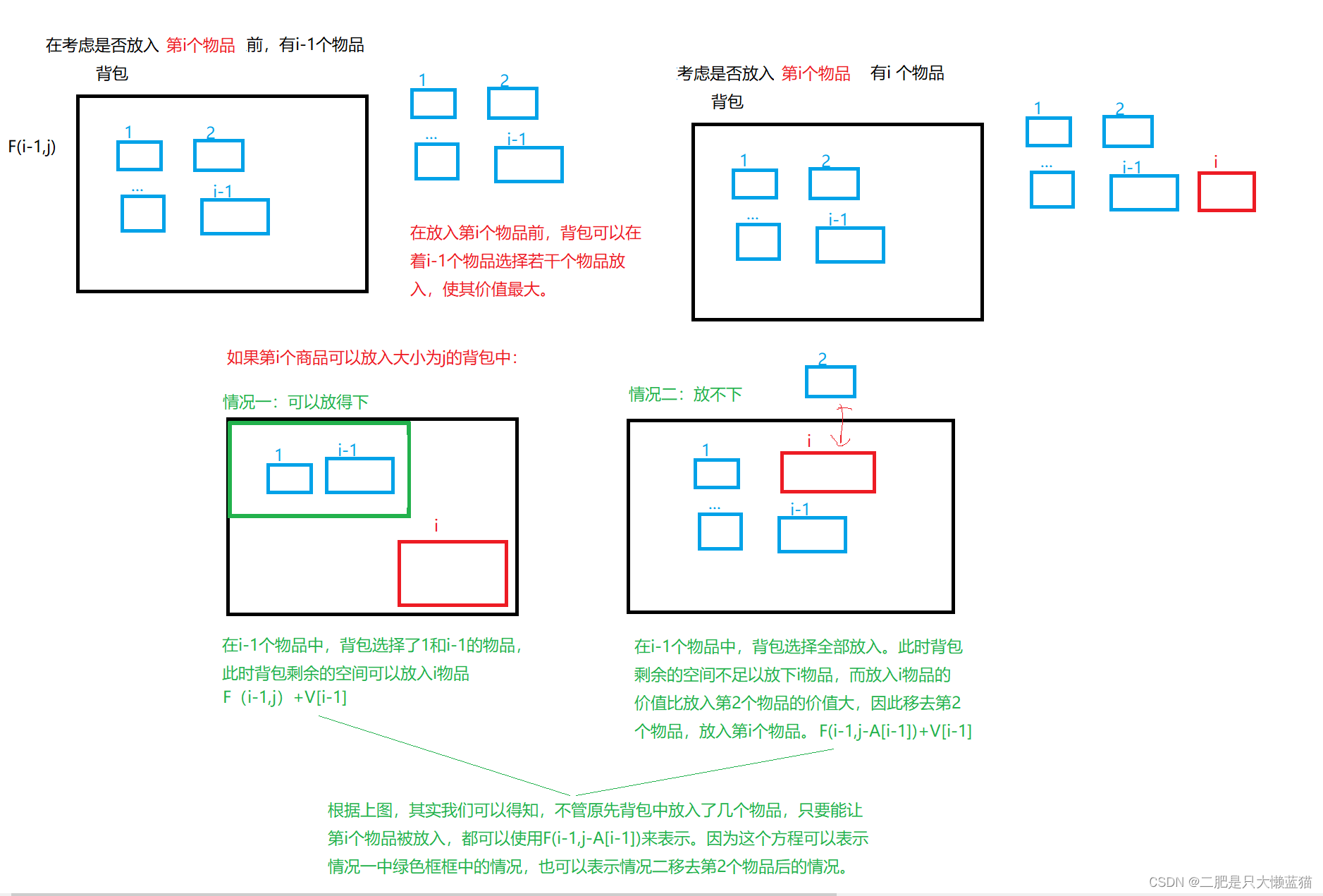
特殊情况：如果装不下，那么此时的价值和前i-1个情况的价值是一样的，即F(i,j) = F(i-1,j);

如果可以装入：需要在两种选择中找最大的，即F(i, j) = max{F(i-1,j), F(i-1, j - A[i]) + V[i]}。

其中，F(i-1,j): 表示不把第i个物品放入背包中， 所以它的价值就是前i-1个物品放入大小为j的背包的最大价值。F(i-1, j - A[i]) + V[i]：表示把第i个物品放入背包中，价值增加V[i],但是需要腾出j - A[i]的大小放第i个商品。

初始化：第0行和第0列都为0，表示没有装物品时的价值都为0，即F(0,j) = F(i,0) = 0;

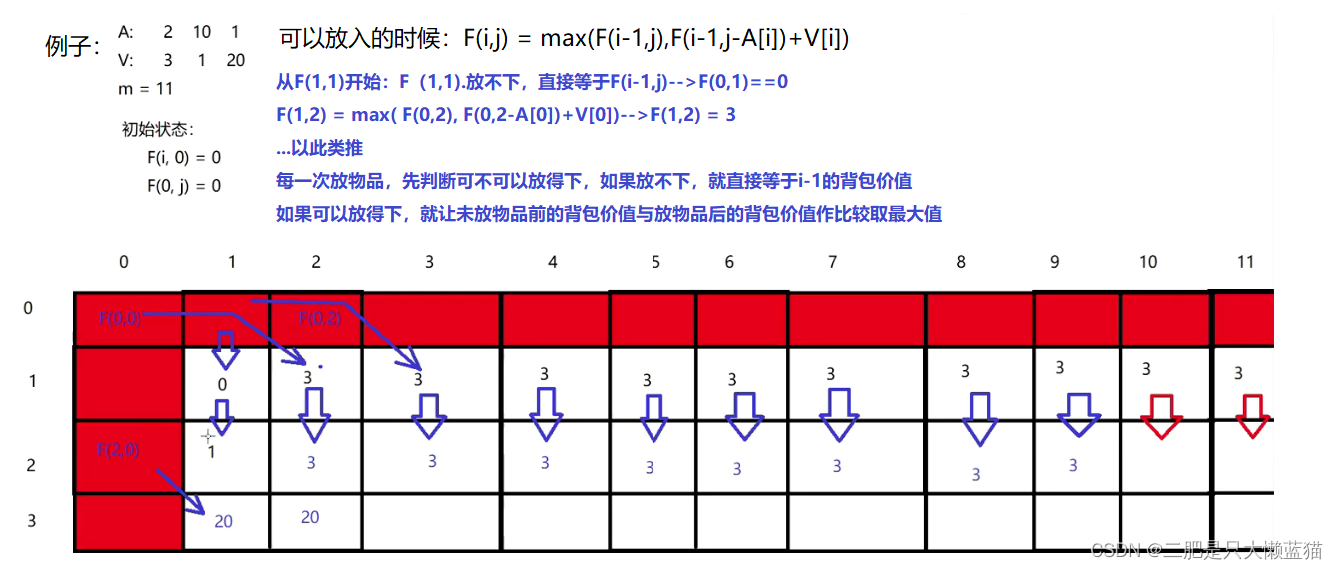
返回值：F(n,m);

代码如下：

int backPackII(int m, vector &a, vector &v) {// write your code hereif(a.empty() || v.empty() || m< 1){return 0;}//多加一行一列，用于设置初始条件int N = a.size()+1;int M = m+1;vector> ret(N,vector(M,0));for(int i = 1;ij){ret[i][j] = ret[i-1][j];}else //装得下，放或不放{//如果不放，那价值也跟i-1的价值一样//如果放，需要腾出放物品i的空间ret[i][j] = max(ret[i-1][j],ret[i-1][j-a[i-1]]+v[i-1]);}}}return ret[N-1][m];}

优化：

上面的算法在计算第i行元素时，只用到第i-1行的元素，所以二维的空间可以优化为一维空间。但是如果是一维向量，需要从后向前计算，因为后面的元素更新需要依靠前面的元素未更新（模拟二维矩阵的上一行的值）的值。

int backPackII(int m, vector A, vector V) {if (A.empty() || V.empty() || m < 1) {return 0;} const int N = A.size();//多加一列，用于设置初始条件，因为第一件商品要用到前面的初始值const int M = m + 1;vector result;//初始化所有位置为0，第一行都为0，初始条件result.resize(M, 0);//这里商品的索引位置不需要偏移，要和未优化的方法区分开
//这里的i-1理解为上一行，或者未更新的一维数组值for (int i = 0; i != N; ++i){for (int j = M - 1; j > 0; --j) {//如果第i个商品大于j,说明放不下， 所以(i,j)的最大价值和(i-1,j)相同if (A[i] > j) {result[j] = result[j];} //如果可以装下，分两种情况，装或者不装//如果不装，则即为(i-1, j)//如果装，需要腾出放第i个物品大小的空间： j - A[i]// 装入之后的最大价值即为(i - 1, j -A[i - 1]) + 第i个商品的价值V[i]//最后在装与不装中选出最大的价值else {int newValue = result[j - A[i]] + V[i];result[j] = max(newValue, result[j]);}}} //返回装入前N个商品，物品大小为m的最大价值return result[m];
};