为什么要使用三元查找

通过引入三元搜索算法，最大限度地提高您的搜索能力并降低时间复杂性。可以将本文看作是使用不太为人所知但非常有效的算法(即三元搜索)来解锁高效搜索的功能。

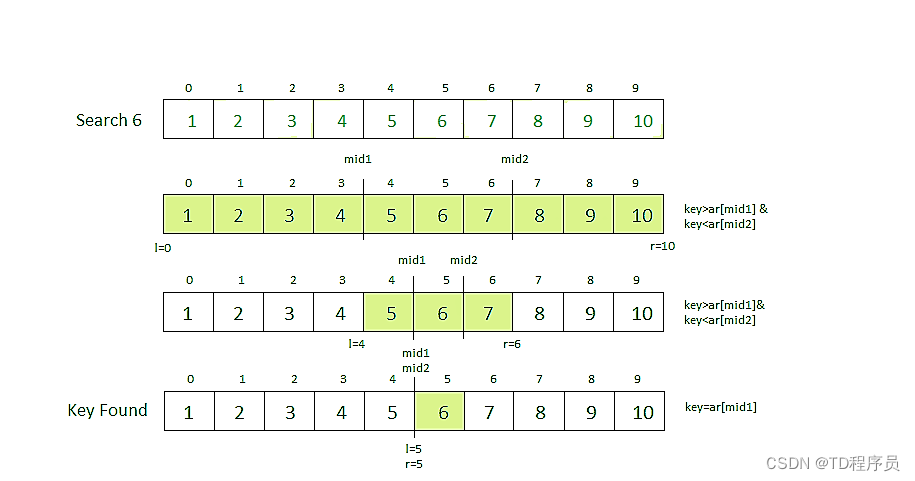
三元搜索是一种减少(通过常数)和征服算法，可用于查找数组中的元素。它类似于二分法搜索，我们将数组分为两部分，但在这个算法中，我们将给定的数组分为三部分，并确定哪个具有键(搜索元素)。我们可以通过取mid1和mid2将数组分为三部分，计算如下所示。最初，l和r将分别等于0和n-1，其中n是数组的长度。

它和二分查找是一样的。唯一的区别是，它降低了时间复杂度。它的时间复杂度是O(log n以3为底)，二分搜索的时间复杂度是O(log n以2为底)。

mid1 = l + (r-l)/3

mid2 = r – (r-l)/3

注意:数组需要排序才能对其进行三元搜索。

执行三元搜索的步骤:

• 首先，我们将键值与mid1的元素进行比较。如果发现相等，则返回mid1。

• 如果不是，则将键值与mid2处的元素进行比较。如果发现相等，则返回mid2。

• 如果不是，则检查键值是否小于mid1处的元素。如果是，那么回到第一部分。

• 如果不是，则检查键值是否大于mid2处的元素。如果是，那么回到第三部分。

• 如果不是，那么我们回到第二部分(中间部分)。

下图为查找示例图

三元搜索的递归C语言实现

// C program to illustrate
// recursive approach to ternary search#include // Function to perform Ternary Search
int ternarySearch(int l, int r, int key, int ar[])
{if (r >= l) {// Find the mid1 and mid2int mid1 = l + (r - l) / 3;int mid2 = r - (r - l) / 3;// Check if key is present at any midif (ar[mid1] == key) {return mid1;}if (ar[mid2] == key) {return mid2;}// Since key is not present at mid,// check in which region it is present// then repeat the Search operation// in that regionif (key < ar[mid1]) {// The key lies in between l and mid1return ternarySearch(l, mid1 - 1, key, ar);}else if (key > ar[mid2]) {// The key lies in between mid2 and rreturn ternarySearch(mid2 + 1, r, key, ar);}else {// The key lies in between mid1 and mid2return ternarySearch(mid1 + 1, mid2 - 1, key, ar);}}// Key not foundreturn -1;
}// Driver code
int main()
{int l, r, p, key;// Get the array// Sort the array if not sortedint ar[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };// Starting indexl = 0;// length of arrayr = 9;// Checking for 5// Key to be searched in the arraykey = 5;// Search the key using ternarySearchp = ternarySearch(l, r, key, ar);// Print the resultprintf("Index of %d is %d\n", key, p);// Checking for 50// Key to be searched in the arraykey = 50;// Search the key using ternarySearchp = ternarySearch(l, r, key, ar);// Print the resultprintf("Index of %d is %d", key, p);
}

输出:

Index of 5 is 4

Index of 50 is -1

三元搜索的迭代方法C语言实现

// C program to illustrate
// recursive approach to ternary search#include // Function to perform Ternary Search
int ternarySearch(int l, int r, int key, int ar[])
{if (r >= l) {// Find the mid1 and mid2int mid1 = l + (r - l) / 3;int mid2 = r - (r - l) / 3;// Check if key is present at any midif (ar[mid1] == key) {return mid1;}if (ar[mid2] == key) {return mid2;}// Since key is not present at mid,// check in which region it is present// then repeat the Search operation// in that regionif (key < ar[mid1]) {// The key lies in between l and mid1return ternarySearch(l, mid1 - 1, key, ar);}else if (key > ar[mid2]) {// The key lies in between mid2 and rreturn ternarySearch(mid2 + 1, r, key, ar);}else {// The key lies in between mid1 and mid2return ternarySearch(mid1 + 1, mid2 - 1, key, ar);}}// Key not foundreturn -1;
}// Driver code
int main()
{int l, r, p, key;// Get the array// Sort the array if not sortedint ar[] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };// Starting indexl = 0;// length of arrayr = 9;// Checking for 5// Key to be searched in the arraykey = 5;// Search the key using ternarySearchp = ternarySearch(l, r, key, ar);// Print the resultprintf("Index of %d is %d\n", key, p);// Checking for 50// Key to be searched in the arraykey = 50;// Search the key using ternarySearchp = ternarySearch(l, r, key, ar);// Print the resultprintf("Index of %d is %d", key, p);
}

输出:

Index of 5 is 4

Index of 50 is -1