文章目录

• • 136. 只出现一次的数字
  • 137. 只出现一次的数字 II
  • 260. 只出现一次的数字 III
  • 剑指 Offer II 070. 排序数组中只出现一次的数字

136. 只出现一次的数字

• 异或：两个bit运算时，相同为0，相异为1；两个数运算时，任何数和0异或不变

• 交换律：a ^ b ^ c <=> a ^ c ^ b

class Solution {
public:int singleNumber(vector& nums) {// 异或：相同为0，相异为1，任何数和0异或不变，和1异或取反int ans = 0;for(int num : nums) ans ^= num;return ans;}
};

137. 只出现一次的数字 II

class Solution {
public:int singleNumber(vector& nums) {int bit_freq[32] = {0};unsigned int bit = 1;for(int i = 31; i >= 0; i--){for(int num : nums){if(num & bit){bit_freq[i]++;}}bit <<= 1;}int ans = 0;for(int i = 0; i < 32; i++){ans = (ans << 1);ans += bit_freq[i] % 3;}return ans;}
};

把所有的数都用二进制形式表示，用一个长度为32的数组存放每个位1出现的次数，如下：

把目前得到的数组1340 3014，每个元素都模3，余数就是原数组只出现一次数字的二进制表示（1010 0011）将此二进制还原即可

这种方法还可以解决某个元素只出现1次，其他元素出现n次的题型，对n取模即可

恢复二进制表示时，由于bit_freq[0]存放高位，而bit_freq[31]存放低位，所以从bit_freq[0]开始恢复，每次将ans左移后再加上bit_freq[i] % 3

260. 只出现一次的数字 III

由于异或运算满足交换律，且相同的数异或为0，任何数和0异或不变，所以整个数组逐元素异或的结果res就是两个只出现一次的a、b相异或的结果res

由于a、b两个数字不一样，所以异或的结果不为0，我们找到res的二进制表示中第一个为1的bit（这个bit表示a、b对应位置的bit异或结果位1，即a、b该位置的bit不同），以这个bit是否为1，将整个数组分为两部分，这样相同的数肯定分在两个数组中，而a、b肯定不在一个数组中

数组中所有元素都出现2次，求出只出现一次的数字，整个数组逐元素相异或即可

class Solution {
public:vector singleNumber(vector& nums) {int n = nums.size();if(n < 3) return nums;int res = 0;for(int num : nums) res ^= num;int bit = 1;while((res & bit) == 0){bit <<= 1;}int ans1 = 0;int ans2 = 0;for(int num : nums){if(num & bit) ans1 ^= num;else ans2 ^= num;}return {ans1, ans2};}
};

剑指 Offer II 070. 排序数组中只出现一次的数字

class Solution {
public:int singleNonDuplicate(vector& nums) {int ans = 0;for(int num : nums){ans ^= num;}return ans;}
};

二分查找

正常情况下，如果没有那个只出现一次的数字，所有的数应该先出现在偶数下标，再出现在奇数下标，比如：

一旦出现了那个只出现一次的数字，后面所有的数字都会先在奇数下标出现，后出现在偶数下标，比如：

首先我们要知道，最终只出现一次的那个数字一定在偶数下标

我们使用二分查找，mid下标分为以下四种情况：

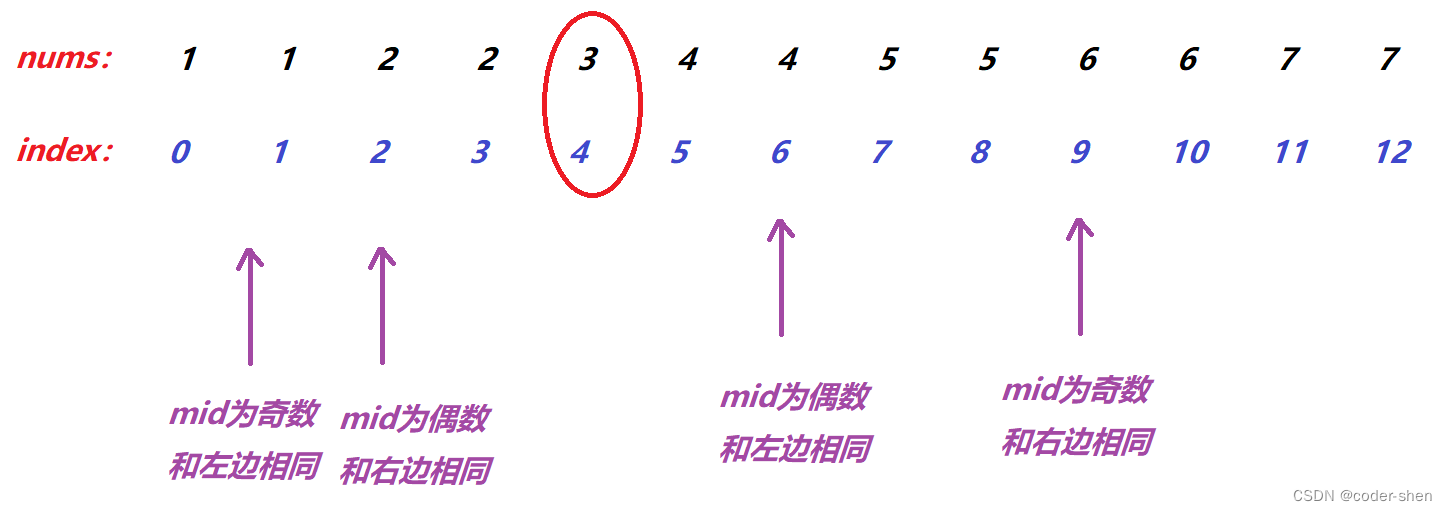
• mid为奇数，和左边相同：答案在右边
• mid为奇数，和右边相同：答案在左边
• mid为偶数，和左边相同：答案在左边
• mid为偶数，和右边相同：答案在右边
• mid为偶数，和左右两边都不同，mid就是答案

class Solution {
public:int singleNonDuplicate(vector& nums) {int l = 0;int r = nums.size() - 1;int ans;while (l <= r) {int mid = l + ((r - l) >> 1);if (mid & 1) {if (nums[mid] == nums[mid - 1]) l = mid + 1;else r = mid - 1;}else {if (mid > 0 && nums[mid] == nums[mid - 1]) r = mid - 1;else if (mid < nums.size() - 1 && nums[mid] == nums[mid + 1]) l = mid + 1;else {ans = nums[mid];break;}}}return ans;}
};