【问题描述】

​ 蓝桥学院由21栋教学楼组成，教学楼编号1到21。对于两栋教学楼a和b，当a和b互质时，a和b之间有一条走廊直接相连，两个方向皆可通行，否则没有直接连接的走廊。
​ 小蓝现在在第一栋教学楼，他想要访问每栋教学楼正好一次，最终回到第一栋教学楼(即走一条哈密尔顿回路)，请问他有多少种不同的访问方案?两个访问方案不同是指存在某个i，小蓝在两个访问方法中访问完教学楼i后访问了不同的教学楼。
​ 提示:建议使用计算机编程解决问题。

【答案提交】

​ 这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

解析：

一、分析

1. 本题的第一想法就是暴力求解即深度优先搜索，但是时间复杂度是O(nn)O(n^n)O(nn)，超过15就求解不了，电脑罢工。因此靠这种方法是不行的。
   1. 时间复杂度计算：n×n×n......×n=nnn\times n\times n......\times n=n^nn×n×n......×n=nn
2. 如果优化上面这个题目呢？使用带剪枝的回溯法，但是因为是计数问题，不是求解最优化问题，所以不行。
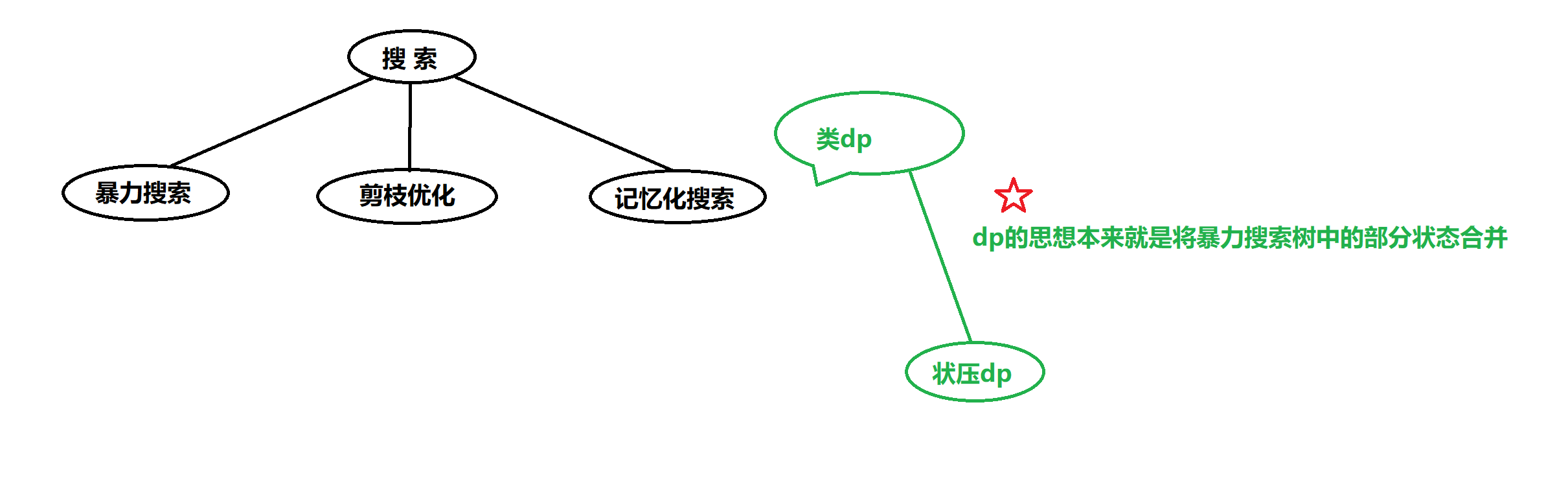
3. 记忆化搜索（类dp）,21<32，2212^{21}221能被intintint表示，状压dp。

总结：

二、解题

• 看到21能想到状压dp，正好2的21次int能存下，先尝试使用 dp[221]dp [2 ^ {21}]dp[221]一维数组，转换成2进制后1代表访问过，0代表没访问过，可以表示所有点是否被访问的状态，dp[state]存有多少种方式可以形成状态state。
• 发现状态转移方程无法表示，比如状态11101到状态11111，如果路径为1-3-5-4，则不能和2连通，而路径1-3-4-5就可以接着访问2，只有dp[11101]中的一部分可以为dp[11111]所用，因此dp[11111]不能用dp[11101]推出。—遇到了问题
  • dp[11101]可以是状态1：1->3->4->5，可以是状态2：1->4->3->5,可以是…等。所以说dp的思想本来就是将暴力搜索树中的部分状态合并
  • 搜索就是遍历所有可能的情况，部分状态不能合并
  • 但是dp的思想就是将暴力搜索树中的部分状态合并，并记录下来，所以相对于搜索，dp做了两件事：①记录；②合并
• 该问题不仅和是否访问有关，还和访问顺序有关。使用一维数组只记录下了访问节点，并没有访问顺序，所以再开一维用以记录顺序。
  • 根据题意互质的结点才相连，在状态10111下路径1-2-3-5和路径1-3-2-5虽然顺序不同，但是最后的5号点都是能和4相连，导出状态11111；还是状态10111，1-3-5-2和路径1-5-3-2都不能和4相连，不能导出状态11111，我们只需要再加一个最末位置，就可以分割开这两种情况。
  • 同时把1-2-3-5与1-3-2-5合并为一个状态 dp[10111][5] ， 1-3-5-2与1-5-3-2合并为一个状态 dp[10111][2] ，而dp[11111]中的dp[11111][4]=dp[10111][5]+dp[10111][3]，于是顺其自然的也推出了状态转移方程。
  • 最后访问4的状态数量等于倒数第2个访问3的路径数加上和倒数第二个访问5的路径数。
• dp[i][j]=dp[i−(1<

public static int gcd(int a,int b){return b==0?a:gcd(b,a%b);
}

dp[1][0]=1;

public class ExaminationE_dpVersion3 {public static final int n = 21;//判断是否互质public static int gcd(int a,int b){return b==0?a:gcd(b,a%b);}public static long[][] allPath(long[][] dp,long[][] path){for (int i = 0; i < (1 << n); i++) {for (int j = 0; j < n; j++) {if (((i>>j)&1)==1) {for (int k = 0; k < n; k++) {if (path[j][k]==1&&(((i-(1<>k)&1)==1) {dp[i][j] += dp[i-(1<long[][] path = new long[n][n];long[][] dp = new long[1 << n][n];for (int i = 0; i < n; i++) {for (int j = 0; j <= i; j++) {if (gcd(i+1,j+1)==1) {path[i][j] = path[j][i] =  1;}}}//初始化dp[1][0] = 1;long[][] result = allPath(dp,path);long res = 0;for (int i = 1; i < n; i++) {res+=result[(1<