如果某一个问题有很多重叠子问题，使用dp是最有效的。

动态规划中每个状态一定由上一个状态推导而来。

动规五部曲：

1. 确定dp数组以及下标的含义；

2. 确定递推公式；

3. dp数组的初始化；

4. 确定遍历顺序；

5. 举例验证dp数组

基础问题

斐波那契数

爬楼梯

使用最小花费爬楼梯

选择从下标0或下标1开始爬楼梯，也就是说刚开始不产生花费，dp_0=0,dp_1=0。其余部分与爬楼梯类似。

不同路径

m*n的网格，与爬楼梯类似，可以用一维的滚动数组进行空间复杂度上优化

不同路径II

m*n的网格，有阻碍，在初始化时注意阻碍只要出现，从它开始后面就都得是0了；

还有一个测试用例是只有一格，刚开始就有阻碍。。。

整数拆分

有个结论，尽可能的拆成3，可以让乘积最大（最后剩余4的时候不再拆成3和1）

不同的二叉搜索树

以n=3为例，当主节点为1时，左孩子无，右孩子有两个节点，于是为dp[0]*dp[2]；

当主节点为2时，左右孩子都只有一个节点，dp[1]*dp[1]；

当主节点为3时，右孩子无，左孩子有两个节点，于是dp[2]*dp[0]。最后将这些相加便是dp[3]。

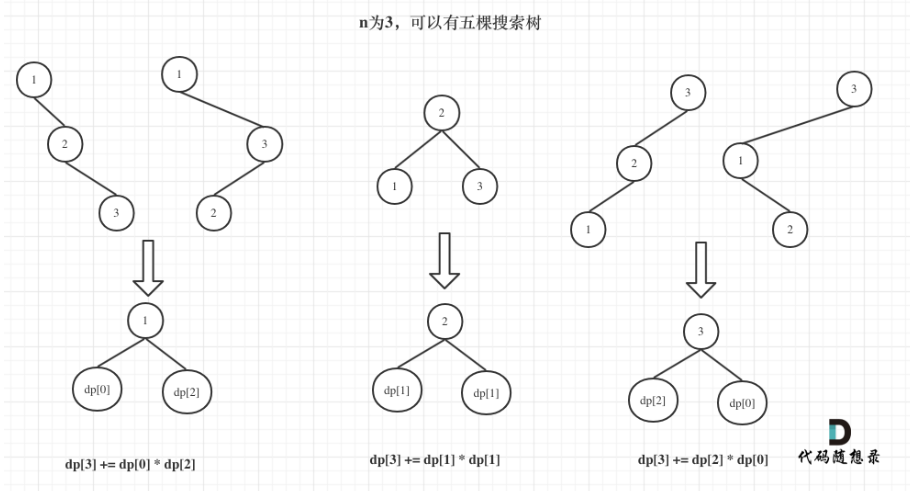
递推关系式为：

dp[i]+=dp[以j为头节点左子树节点数]*dp[以j为头节点右子树节点数]。

j相当于头节点元素，从1遍历到i

dp[i]+=dp[j-1]*dp[i-j]

背包问题

0-1背包问题

有n个物品和最多能背重量为w的背包，第i件物品的重量是weight[i]，价值是value[i]，每件物品只能使用一次，求解哪些物品放入背包价值最大。

例如：

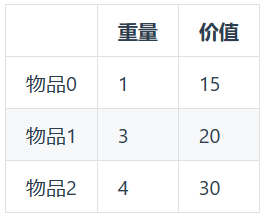
1. 确定dp数组以及下标的含义

dp[i][j]表示从下标0-i的物品里任意取，放进容量为j的背包，价值总和最大为dp[i][j]

2. 确定递推关系式

可以从两个方向推导出dp[i][j]

• 不放物品i 背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]

• 放物品i d p[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，

那么dp[i - 1][j - weight[i]] + value[i] （物品i的价值），就是背包放物品i得到的最大价值

3. dp数组的初始化

背包容量为0时，一定为0；由递推关系可知i状态的价值由i-1状态推导而来，所以物品0的状态都需要初始化，即dp[0][j]

4. 确定遍历顺序 先物品再背包

5. 举例验证dp数组

滚动数组

1. 确定dp数组的含义及其下标 dp[j]表示容量为j的背包，所背物品价值最大dp[j]

2. 一维dp数组的递推公式 dp[j]=max(dp[j],dp[j-weight[i]]+value[i])

3. 一维数组的初始化

4. 一维dp数组的遍历顺序 先物品后背包 背包倒序

5. 举例验证dp数组

分割等和子集

将数组分割成相等的两个子集，也就是说在数组中任意取如果能取到和为sum/2，则表示可以分。

于是题目转化为：能否在子集中找到和为sum/2的组合。

递推关系式：dp[j]=max(dp[j],dp[j-nums[i]]+nums[i])；

dp[j]表示背包总容量为j时，此时的和为dp[j]，如果dp[sum/2]==sum/2的话，就表示可以找到。

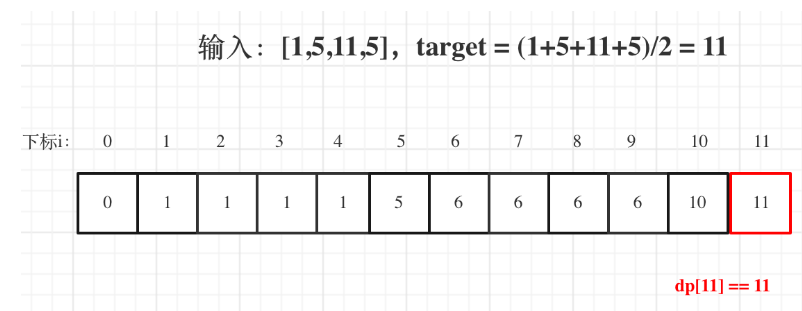
最后一块石头的重量II

将石头尽可能的分成两堆相等的数组,这样相减后才最小。

最后dp[target]里是容量为target的背包所能背的最大重量,那么分成两堆石头，一堆石头的总重量是dp[target]，另一堆就是sum - dp[target]。在计算target的时候，target = sum / 2 因为是向下取整，所以sum - dp[target] 一定是大于等于dp[target]的。那么相撞之后剩下的最小石头重量就是 (sum - dp[target]) - dp[target]。

目标和

left+right=sum

left-right=target，那么left=(sum+target)/2。问题转为装满背包容量为left的背包有多少种装法。

递推关系式：

在已有nums[i]的情况下，有dp[j-nums[i]]种方法凑成dp[j]

递推关系式：dp[j]+=dp[j-nums[i]]。

一和零

strs相当于物品，m个0与n个1表示两个维度的背包容量。

dp[i][j]：最多有i个0和j个1的strs的最大子集的大小为dp[i][j]；

递推关系式：dp[i][j]=max(dp[i][j],dp[i-zeroNum][j-oneNum]+1)。

完全背包问题

有N个物品和最多能被重量为w的背包，每个物品都有无限个（可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。

01背包和完全背包的唯一不同就体现在：遍历顺序上 先物品后背包 背包正序

零钱兑换II

完全背包的装满背包最多有多少种方法问题。

求的是组合个数，于是在遍历顺序上先物品后背包。

组合总和IV

求排列的话，在遍历顺序上先背包后物品。

爬楼梯（进阶版）

改为：一步一个台阶，两个台阶，三个台阶，.......，直到 m个台阶。问有多少种不同的方法可以爬到楼顶呢？

排列问题，在做先背包后物品时发现：

for(int j=1;j<=n;j++){for(int i=0;i<=m;i++){if(j-i>=0) dp[j]+=dp[j-i];}
}

装满背包的最小数量问题

零钱兑换

dp[j]表示背包容量为j时最小的硬币数。

注意这里的初始化：因为最大值INT_MAX，dp[0]=0，并且只有dp[j-coins[i]]!=INT_MAX时才能加上去。

递推关系式：dp[j]=min(dp[j],dp[j-coins[i]]+1)

完全平方数

完全背包的组合问题，与零钱兑换类似。

单词拆分

如果用回溯的话，aaaaaaa，aaaa这样的恶心测试用例过不了，如果加上记忆化递归可以AC，

使用memory数组保存每次计算的以startIndex起始的计算结果，如果memory[startIndex]里已经被赋值了，直接用memory[startIndex]的结果。

下面是动规部分：

单词是物品，字符串s是背包，单词能否组成s，就是问物品能不能把背包装满。（这种问题的转换很重要啊，感觉最缺少的就是这种意识）

dp[j]表示字符串长度为j时，字符串s能否被单词组成。

递推关系式：物品表示：从i=0开始，i

多重背包问题

有N种物品，和容量为V的背包，第i种物品最多有Mi件可用，每件耗费空间是Ci，价值是Wi，求解如何装总价值最大？

其实和0-1背包问题很像，将每件物品的Mi件都摊开，就变成了0-1背包问题。

背包问题的递推关系式小结：

1、能否装满背包或最多能装多少(能否达到目标和)：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i])

2、装满背包有多少种方法：dp[j] += dp[j - nums[i]]

3、装满背包的最大价值：dp[j] = max(dp[j], dp[j - weight[i]] + value[i])

4、装满背包的最小数量:dp[j] = min(dp[j - coins[i]] + 1, dp[j])

遍历顺序问题上：

打家劫舍问题

打家劫舍