1 循环神经网络的原理

1.1 全连接神经网络的缺点

现在的任务是要利用如下语料来给apple打标签：
第一句话：I like eating apple！（我喜欢吃苹果！）
第二句话：The Apple is a great company！（苹果真是一家很棒的公司！）
第一个apple是一种水果，第二个apple是苹果公司。
全连接神经网络没有利用上下文来训练模型，模型在训练的过程中，预测的准确程度，取决于训练集中哪个标签多一些，如果水果多，就打上水果的标签，如果苹果公司多，就打上苹果公司；显然这样的模型不能对未知样本进行准确的预测。

1.2 RNN的结构和原理

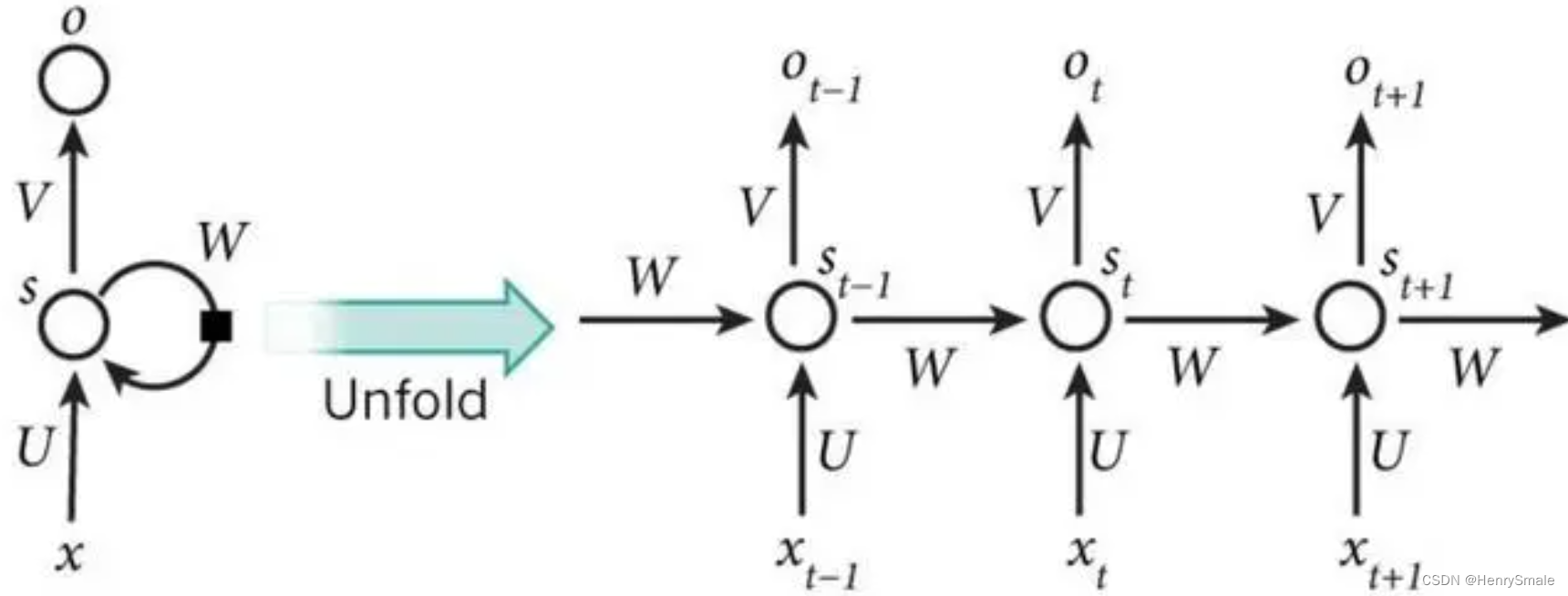
左图如果不考虑WWW，就是一个全连接神经网络：

• 输入层：向量xxx，假设维度为3；
• 隐藏层：向量sss，假设维度为4；
• 输出层：向量ooo，假设维度为2;
• UUU：输入层到隐藏层的参数矩阵，维度为3×43 \times 43×4；
• VVV：隐藏层到输出层的参数矩阵，维度为4×24 \times 24×2。

如果考虑WWW，可以展开为右图：

• xt−1x_{t-1}xt−1​：表示t−1t-1t−1时刻的输入；
• xtx_{t}xt​：表示ttt时刻的输入；
• xt+1x_{t+1}xt+1​：表示t+1t+1t+1时刻的输入；
• WWW：每个时间点的权重矩阵；
• oto_tot​：表示ttt时刻的输出；
• sts_tst​：表示ttt时刻的隐藏层；

核心公式如下：
ot=g(V⋅st)st=f(U⋅xt+W⋅st−1)\begin{array}{l} o_{t}=g\left(V \cdot s_{t}\right) \\ s_{t}=f\left(U \cdot x_{t}+W \cdot s_{t-1}\right) \end{array} ot​=g(V⋅st​)st​=f(U⋅xt​+W⋅st−1​)​
循环神经网络的核心思想就是输出oto_tot​不仅仅与xtx_txt​有关，还与xt−1x_{t-1}xt−1​及前序时刻的输入有关。

1.3 RNN的缺点

每一时刻的隐藏状态都不仅由该时刻的输入决定，还取决于上一时刻的隐藏层的值，如果一个句子很长，到句子末尾时，它将记不住这个句子的开头的内容详细内容。详细分析见https://zhuanlan.zhihu.com/p/76772734。

2 LSTM的原理

LSTM是高级的RNN，与RNN的主要区别在于：

• RNN每个时刻都会把隐藏层的值存下来，到下一时刻再拿出来使用，RNN没有挑选的能力；
• LSTM不一样，它有门控装置，会选择性的存储信息；

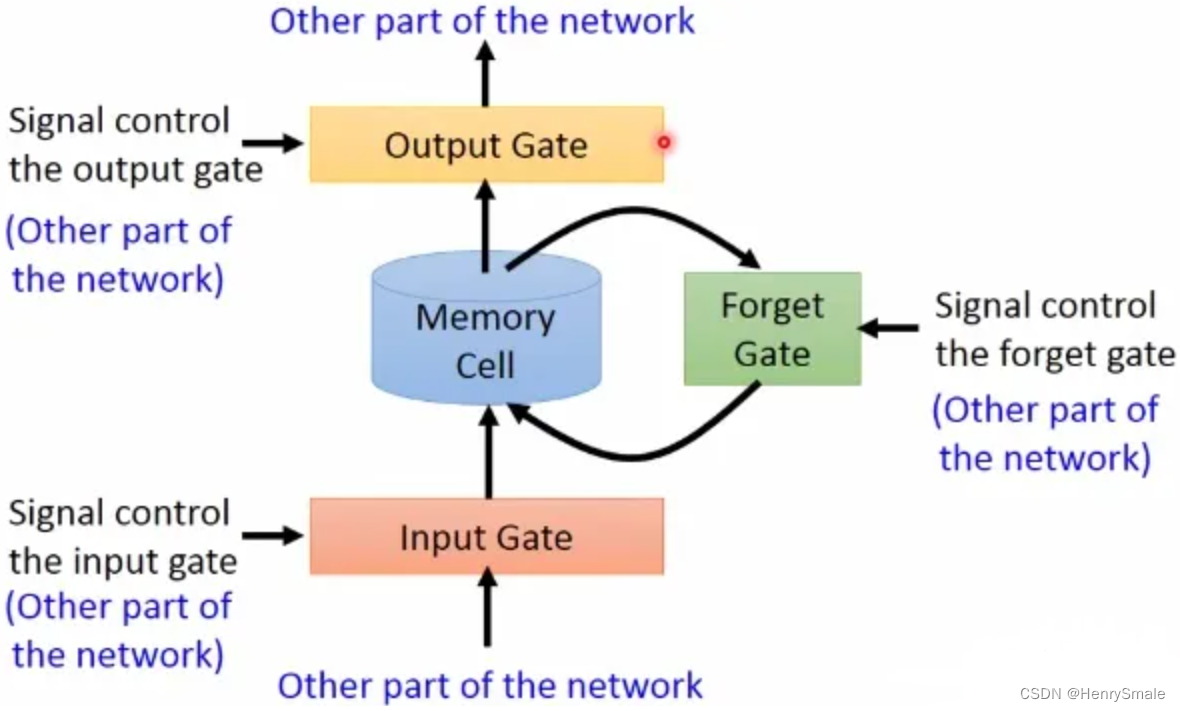
从上图可以看到，LSTM多了三个门：输入门，遗忘门，输出门。

• 输入门：在每一时刻输入的信息首先经过输入门，输入门的开关决定这一时刻是否会将信息输入到Memory Cell；
• 输出门：每一时刻是否有信息从Memory Cell输出取决于这一道门；
• 遗忘门：每一时刻Memory Cell里的值都会经历一个是否被遗忘的过程。

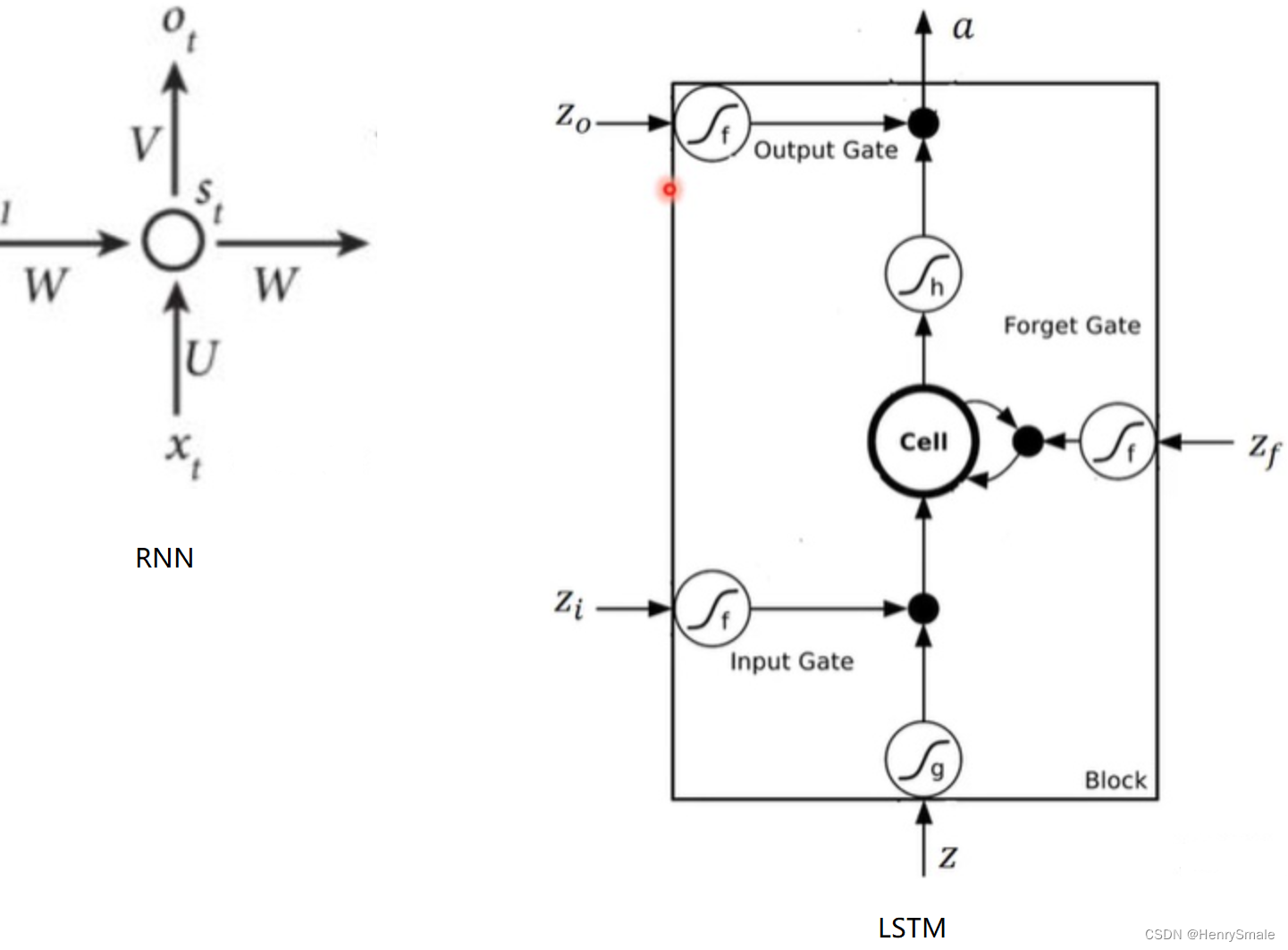
将一个时间点上RNN和LSTM内部结构进行对比，就可以看出两者的区别：

• Cell：类似于RNN的sts_tst​，用来将信息存储到下一时刻，在此用hth_tht​表示ttt时刻的隐藏层；
• aaa：类似于RNN的oto_tot​；
• ∫g,∫h,∫f\int_g, \int_h, \int_f∫g​,∫h​,∫f​：都表示激活函数，LSTM有两个激活函数，一个是tanh，一个是sigmoid；
• Z,Zi,Zf,ZoZ, Z_i, Z_f, Z_oZ,Zi​,Zf​,Zo​：都与输入xtx_txt​有关；

Z=tanh⁡(W[xt,ht−1])Zi=σ(Wi[xt,ht−1])Zf=σ(Wf[xt,ht−1])Zo=σ(Wo[xt,ht−1])\begin{gathered} Z=\tanh \left(W\left[x_t, h_{t-1}\right]\right) \\ Z_i=\sigma\left(W_i\left[x_t, h_{t-1}\right]\right) \\ Z_f=\sigma\left(W_f\left[x_t, h_{t-1}\right]\right) \\ Z_o=\sigma\left(W_o\left[x_t, h_{t-1}\right]\right) \end{gathered} Z=tanh(W[xt​,ht−1​])Zi​=σ(Wi​[xt​,ht−1​])Zf​=σ(Wf​[xt​,ht−1​])Zo​=σ(Wo​[xt​,ht−1​])​

• ZZZ：普通的输入，可以从上面的公式可以得到，ZZZ通过该时刻的输入xtx_txt​ 和上一时刻存在memory cell里的隐藏层信息ht−1h_{t-1}ht−1​向量拼接，再与权重参数向量WWW点积，得到的值经过激活函数tanh最终会得到一个数值。特别注意只有ZZZ的激活函数是tanh，因为ZZZ是真正作为输入的，其他三个都是门控装置。
• ZiZ_iZi​：通过该时刻的输入xtx_txt​和上一时刻隐藏状态ht−1h_{t-1}ht−1​向量拼接，在与权重参数向量WiW_iWi​点积（注意每个门的权重向量都不一样）。得到的值经过激活函数sigmoid的最终会得到一个0-1之间的一个数值，用来作为输入门的控制信号，1表示该门完全打开，0表示该门完全关闭。ZfZ_fZf​和ZoZ_oZo​类似。

2.1 输入门

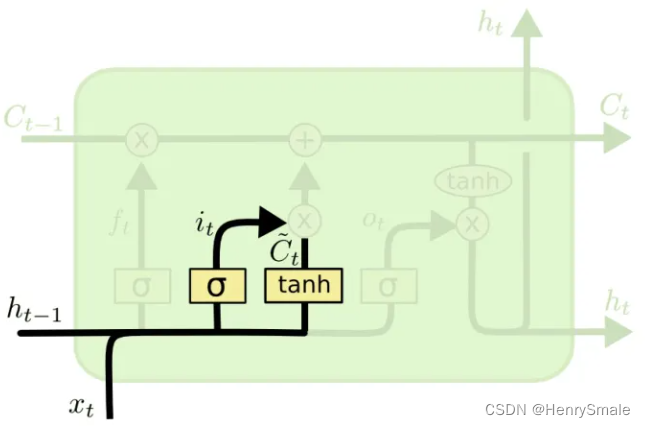
it=σ(Wi⋅[ht−1,xt]+bi)C~t=tanh⁡(WC⋅[ht−1,xt]+bC)\begin{aligned} i_t & =\sigma\left(W_i \cdot\left[h_{t-1}, x_t\right]+b_i\right) \\ \tilde{C}_t & =\tanh \left(W_C \cdot\left[h_{t-1}, x_t\right]+b_C\right) \end{aligned} it​C~t​​=σ(Wi​⋅[ht−1​,xt​]+bi​)=tanh(WC​⋅[ht−1​,xt​]+bC​)​

这个门有两个部分：

• C~t\tilde{C}_tC~t​：这个可以看作是新的输入带来的信息，tanh这个激活函数将内容归一化到-1到1；
• iti_tit​：结构和遗忘门一样的，可以看作是新的信息保留哪些部分。

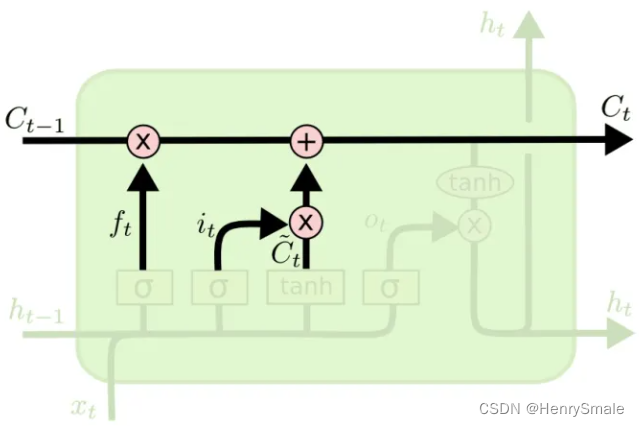
2.2 输出门

2.3 遗忘门

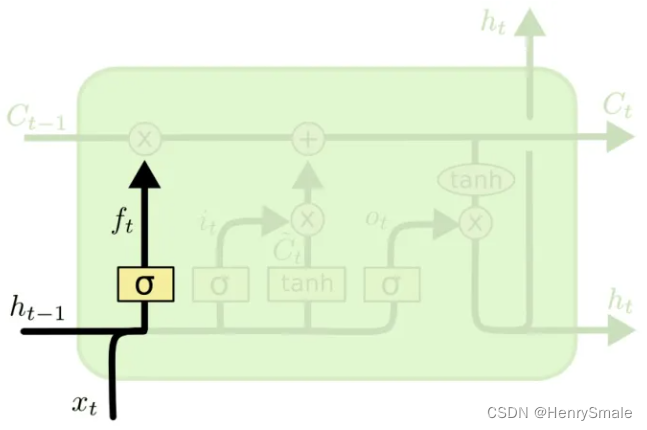
ft=σ(Wf⋅[ht−1,xt]+bf)f_t = \sigma(W_f \cdot [h_{t-1}, x_t] +b_f) ft​=σ(Wf​⋅[ht−1​,xt​]+bf​)
首先说一下[ht−1​,xt​][h_{t−1​},x_t​][ht−1​​,xt​​]这个东西就代表把两个向量连接起来（操作与numpy.concatenate相同）。然后ftf_tft​​就是一个网络的输出，看起来还是很简单的，执行的是上图中的公式。 具体的操作如下图所示：

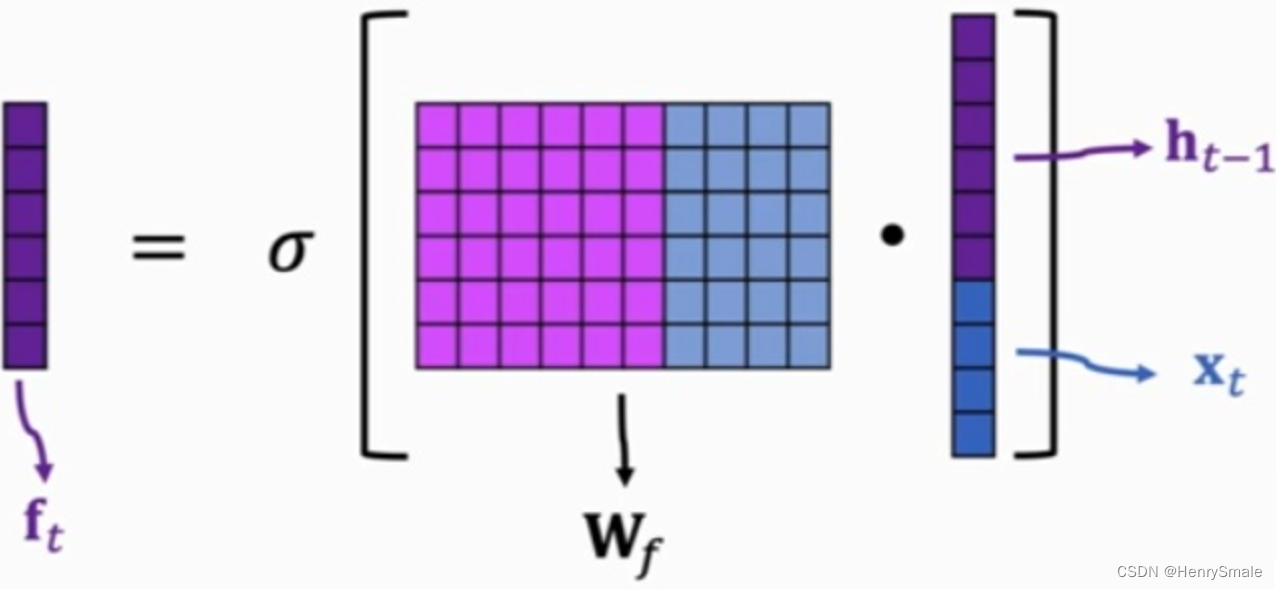
为什么称为遗忘门呢？因为σ\sigmaσ的输出在0到1之间，这个输出 ftf_tft​逐位与Ct−1C_{t-1}Ct−1​的元素相乘，当ftf_tft​的某一位的值为0的时候，这Ct−1C_{t-1}Ct−1​对应位的信息被去掉，而值为(0, 1)，对应位的信息就保留了一部分，只有值为1的时候，对应的信息才会完整的保留。

3 相关应用

3.1 语音识别

A. Graves, A. Mohamed and G. Hinton, Speech Recognition with Deep Recurrent Neural Networks, arXiv:1303.5778

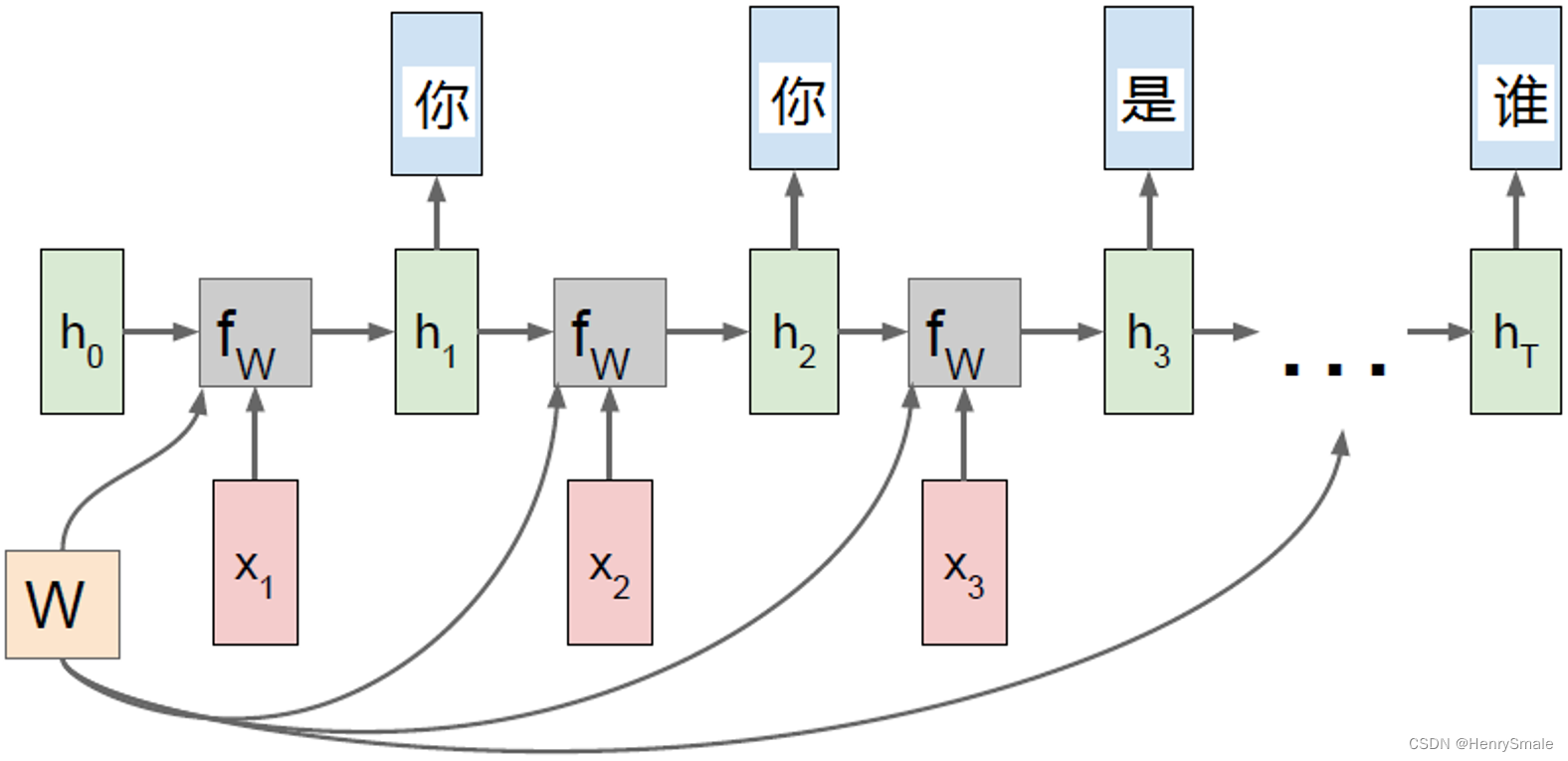
输入特征向量，输出对应的文字。用RNN进行Triphone的识别，在TIMIT数据集上获得了比DNN-HMM更高的识别率。

3.2 文本生成

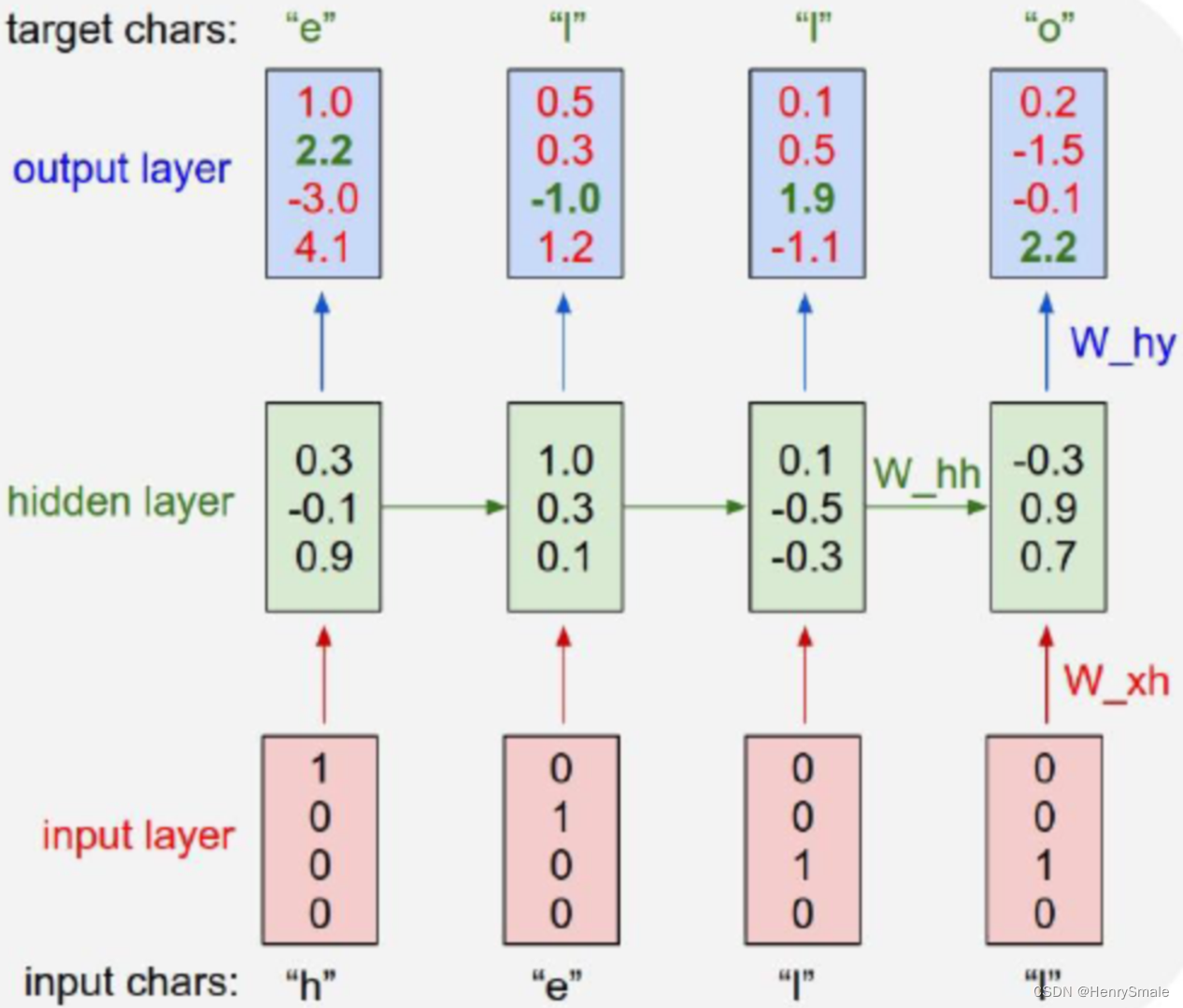
训练样本：中国古诗集

• 首春: 寒随穷律变，春逐鸟声开。初风飘带柳，晚雪间花梅。碧林青旧竹，绿沼翠新苔。芝田初雁去，绮树巧莺来。
• 初晴落景: 晚霞聊自怡，初晴弥可喜。日晃百花色，风动千林翠。池鱼跃不同，园鸟声还异。寄言博通者，知予物外志。
• 初夏: 一朝春夏改，隔夜鸟花迁。阴阳深浅叶，晓夕重轻烟。哢莺犹响殿，横丝正网天。珮高兰影接，绶细草纹连。碧鳞惊棹侧，玄燕舞檐前。何必汾阳处，始复有山泉。
• 度秋: 夏律昨留灰，秋箭今移晷。峨嵋岫初出，洞庭波渐起。桂白发幽岩，菊黄开灞涘。运流方可叹，含毫属微理。

3.3 图像注释

O. Vinyals et al. Show and tell: A neural image caption generator, arXiv:1411.4555v1, 2014.
输入：图像；
输出：描述性文字。

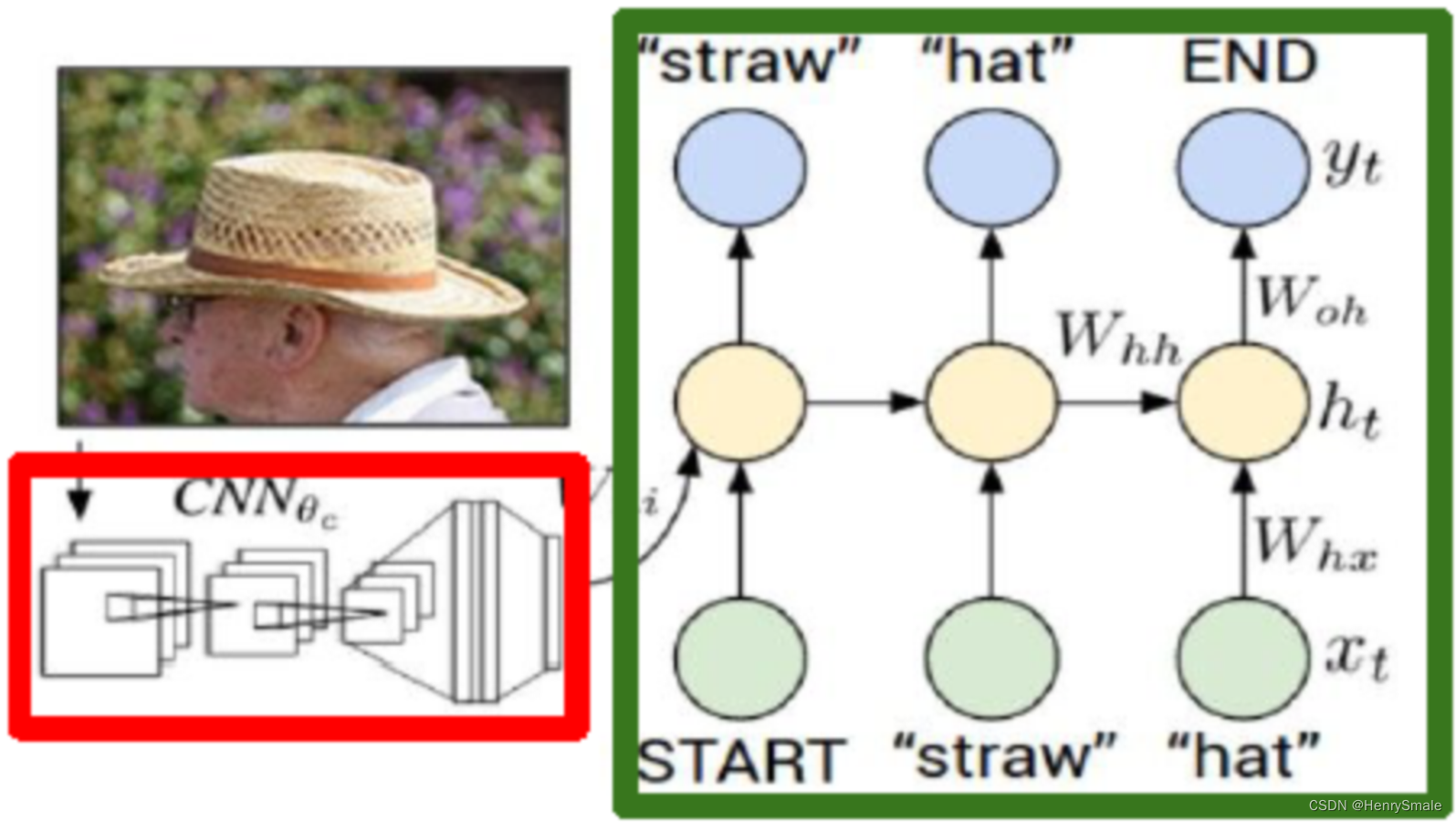
描述准确的例子：

描述不准确的例子：

4 代码分析

用RNN来实现一个八位的二进制数加法运算。
代码实现地址：
http://iamtrask.github.io/2015/11/15/anyone-can-code-lstm/

import copy, numpy as np
np.random.seed(0)
# sigmoid函数
def sigmoid(x):output = 1 / (1 + np.exp(-x))return output
# sigmoid导数
def sigmoid_output_to_derivative(output):return output * (1 - output)
# 训练数据生成
int2binary = {}
binary_dim = 8
largest_number = pow(2, binary_dim)
binary = np.unpackbits(np.array([range(largest_number)], dtype=np.uint8).T, axis=1)
for i in range(largest_number):int2binary[i] = binary[i]
# 初始化一些变量
alpha = 0.1 #学习率
input_dim = 2   #输入的大小
hidden_dim = 8  #隐含层的大小
output_dim = 1  #输出层的大小
# 随机初始化权重
synapse_0 = 2 * np.random.random((hidden_dim, input_dim)) - 1   #(8, 2)
synapse_1 = 2 * np.random.random((output_dim, hidden_dim)) - 1  #(1, 8)
synapse_h = 2 * np.random.random((hidden_dim, hidden_dim)) - 1  #(8, 8)
synapse_0_update = np.zeros_like(synapse_0) #(8, 2)
synapse_1_update = np.zeros_like(synapse_1) #(1, 8)
synapse_h_update = np.zeros_like(synapse_h) #(8, 8)
# 开始训练
for j in range(100000):# 二进制相加a_int = np.random.randint(largest_number / 2)  # 随机生成相加的数a = int2binary[a_int]  # 映射成二进制值b_int = np.random.randint(largest_number / 2)  # 随机生成相加的数b = int2binary[b_int]  # 映射成二进制值# 真实的答案c_int = a_int + b_int   #结果c = int2binary[c_int]   #映射成二进制值# 待存放预测值d = np.zeros_like(c)overallError = 0layer_2_deltas = list() #输出层的误差layer_2_values = list() #第二层的值（输出的结果）layer_1_values = list() #第一层的值（隐含状态）layer_1_values.append(copy.deepcopy(np.zeros((hidden_dim, 1)))) #第一个隐含状态需要0作为它的上一个隐含状态#前向传播for i in range(binary_dim):X = np.array([[a[binary_dim - i - 1], b[binary_dim - i - 1]]]).T    #(2,1)y = np.array([[c[binary_dim - i - 1]]]).T   #(1,1)layer_1 = sigmoid(np.dot(synapse_h, layer_1_values[-1]) + np.dot(synapse_0, X)) #(1,1)layer_1_values.append(copy.deepcopy(layer_1))   #(8,1)layer_2 = sigmoid(np.dot(synapse_1, layer_1))   #(1,1)error = -(y-layer_2)    #使用平方差作为损失函数layer_delta2 = error * sigmoid_output_to_derivative(layer_2)    #(1,1)layer_2_deltas.append(copy.deepcopy(layer_delta2))d[binary_dim - i - 1] = np.round(layer_2[0][0])future_layer_1_delta = np.zeros((hidden_dim, 1))#反向传播for i in range(binary_dim):X = np.array([[a[i], b[i]]]).Tprev_layer_1 = layer_1_values[-i-2]layer_1 = layer_1_values[-i-1]layer_delta2 = layer_2_deltas[-i-1]layer_delta1 = np.multiply(np.add(np.dot(synapse_h.T, future_layer_1_delta),np.dot(synapse_1.T, layer_delta2)), sigmoid_output_to_derivative(layer_1))synapse_0_update += np.dot(layer_delta1, X.T)synapse_h_update += np.dot(layer_delta1, prev_layer_1.T)synapse_1_update += np.dot(layer_delta2, layer_1.T)future_layer_1_delta = layer_delta1synapse_0 -= alpha * synapse_0_updatesynapse_h -= alpha * synapse_h_updatesynapse_1 -= alpha * synapse_1_updatesynapse_0_update *= 0synapse_1_update *= 0synapse_h_update *= 0# 验证结果if (j % 100 == 0):print("Error:" + str(overallError))print("Pred:" + str(d))print("True:" + str(c))out = 0for index, x in enumerate(reversed(d)):out += x * pow(2, index)print(str(a_int) + " + " + str(b_int) + " = " + str(out))print("------------")

参考文献

https://zhuanlan.zhihu.com/p/518848475