1.前言

什么是排序呢？排序就是将一系列物品按照某项标准进行位置的变换。比如，对于数组arr[] = {10，4，2，8，9，20} 来说，如果从小到大排序就是{2，4，8，9，10，20}，从大到小排序就是{20，10，9，8，4，2}。

对于Java来说，如果你只需要实现排序的目标，那么你只需要用下面这段代码就可以了：

package 排序;import java.util.Arrays;
import java.util.Comparator;public class Sort {public static void out(Integer arr[]) {int len = arr.length;for(int i= 0;i(){@Overridepublic int compare(Integer o1, Integer o2) {// TODO 自动生成的方法存根return o2-o1;}}); //降序排序out(arr); //20 10 9 8 4 2 }
}

常见的排序算法有：冒泡排序、选择排序、插入排序、希尔排序、归并排序、快速排序、堆排序、基数排序、计数排序。接下来分别细讲这些排序算法。

2.冒泡排序

冒泡排序是最简单的排序算法，但是他的复杂度达到了O(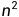),并不算理想。

2.1.算法思路

它的主要排序思路是：重复访问数组中的数据，每次比较相邻的两个数据，如果后一个比较大就交换位置，由于数组中的较小的数会逐渐跑到前面来，像冒泡泡一样，所以被称为冒泡排序。

比如上面的例子，我们每一步每一步的分析：

初始状态： {10，4，2，8，9，20}

第一步：一次比较两个数字：

第一次比较(10 > 4)：{4，10，2，8，9，20}

第二次比较(10 > 2)：{4，2，10，8，9，20}

第三次比较(10 > 8)：{4，2，8，10，9，20}

第四次比较(10 > 9)：{4，2，8，9，10，20}

第五次比较(10 < 20)：{4，2，8，9，10，20}

第二步：再从头来过

第一次比较(4 > 2)：{2，4，8，9，10，20}

第二次比较(4 < 8)：{2，4，8，9，10，20}

.................

就这样循环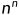 次就可以保证排序成功了。

2.2.代码

    public static int[] bubble_sort(int[] arr) {if(arr == null) {return null;}int len = arr.length;for(int i = 0;i arr[j]) {int tmp  =arr[j-1];arr[j-1] = arr[j];arr[j] = tmp;}}}return arr;}

3.选择排序

3.1.算法思路

选择排序的思路便是，每次从未排序的数组中选择出最小（大）的数，通过交换位置，使它放到已排序的序列的尾部。

比如上面的例子，我们每一步每一步的分析：

初始状态： {10，4，2，8，9，20}

红色表示最小的值，绿色表示要换的位置

第一步：已排序的{} ,未排序的{10，4，2，8，9，20}，选出最小的（红色），与第一个数进行交换得到 {2，4，10，8，9，20}

第二步：已排序的{2，} ,未排序的{4，10，8，9，20}，无需交换，{2，4，10，8，9，20}

第三步：已排序的{2，4} ,未排序的{10，8，9，20} ==同理==> {8，10，9，20}

第四步：已排序的{2，4，8} ,未排序的{10，9，20} ==同理==> {9，10，20}

......

最后：已排序的{2，4，8，9，10，20} ,未排序的{}

3.2.代码

    public static int[] select_sort(int[] arr) {if(arr == null) {return null;}int len = arr.length;for(int i = 0;i < len;i++) {int index = i;int min = arr[i];for(int j = i+1; j< len ;j++) {if(min > arr[j]) { //找最小的值 和下标进行交换min = arr[j];index = j;}}arr[index] = arr[i];arr[i] = min;}return arr;}

4.插入排序

4.1.算法思想

遍历循环数组中的数字，将数字插入到已经排好序的数组中。

比如上面的例子，我们每一步每一步的分析：

初始状态： {10，4，2，8，9，20}

第一步：10前面没有数字，直接插入 {10，4，2，8，9，20}

第二步：4插到10前面：{4，10，2，8，9，20}

第三步：2插到4前面：{2，4，10，8，9，20}

第四步：8插到4 和 10 之间： {2，4，8，10，9，20}

第五步：9插到8和10之间： {2，4，8，9，10，20}

第六步：20插到10之后{2，4，8，9，10，20} 结束

对于插入的步骤，我们要从已排好序的数组从尾部往头部遍历直到不小于当前要插入的值，则该位置就可以插入。

4.2代码

    public static int[] insert_sort(int[] arr) {if(arr == null) {return null;}int len = arr.length;for(int i = 1;i= 0 && currentData < arr[preIndex]) { //找到插入的地方arr[preIndex+1] = arr[preIndex];preIndex--;}arr[preIndex+1] = currentData;}return arr;}

5.希尔排序

5.1.算法思想

插入排序有个不好的地方，就是在找插入的地方的时候，需要一步一步去迭代替换数值，很慢，如果用插入排序来排相对比较有序的数组，那么它就会快很多，因为不会进入代码中的while循环，使得它接近线性复杂度。而希尔排序的诞生就是为了此刻，它是插入排序的加强版，希尔排序先把数组分割成若干个子序列进行插入排序，使得数每次插入排序的时候会比较的有序，降低了复杂度。

比如上面的例子，我们每一步每一步的分析：

初始状态： {10，4，2，8，9，20}

5.2代码

    public static int[] hill_sort(int[] arr) {if(arr == null) {return null;}int len = arr.length;for(int step = len/2;step >= 1;step/=2) {for(int i = step; i= 0 && currentData < arr[preIndex]) {arr[preIndex + step] = arr[preIndex];preIndex -= step;}arr[preIndex+step] = currentData;}}return arr;}

6.归并排序

6.1.算法思想

归并排序是每次利用中间为界限，将数组分割成若干个小组，然后在合并小组的时候顺便排序，是一种分治思想。先分后合并。

6.2代码

public static int[] merge_sort(int[] arr) {if(arr == null) {return null;}if(arr.length == 1) {return arr;}devide(arr,0,arr.length-1);return arr;}private static void devide(int[] arr, int l, int r) {// TODO 自动生成的方法存根int mid = (l+r)/2;if(l < r) {devide(arr,l,mid);devide(arr,mid+1,r);merge(arr,l,mid,r);}}private static void merge(int[] arr, int l, int mid, int r) {// TODO 自动生成的方法存根//合并的过程顺便排序int left = l;int right = mid+1;int tmp[] = new int[r-l+1];int pi = 0;while(left <= mid && right <= r) {//谁比较小谁先进来if(arr[left] > arr[right]) {tmp[pi++] = arr[right++];}else {tmp[pi++] = arr[left++];}}while(left <= mid) {tmp[pi++] = arr[left++];}while(right <= r) {tmp[pi++] = arr[right++];}for(int i = 0;i

7.快速排序

7.1.算法思想

快速排序的算法思想是每次定义数组中一个之作为标准值，一般我们让第一个来做，然后我们将这个数组分为以标准值位界限，左边的数小于这个标准值，右边的数大于这个标准值，然后使用递归分别求出左边的右边的排序。

比如上面的例子，我们每一步每一步的分析：

初始状态： {10，4，2，8，9，20}

第一步： 10为基准 ==> {4，2，8，9} {10} {20}

第二步：使用递归，对于{4，2，8，9} 以4为基准 ===> {2} {4} {8，9} {10} {20}

第三步：还是在递归中，对于{20}只有一个数不用变 ====> {2} {4} {8，9} {10} {20}

第四步：还是在递归中，对于{2}只有一个数不用变 ====> {2} {4} {8，9} {10} {20}

第五步：还是在递归中，对于{8，9} 以8 为基准 ====> {2} {4} {8} {9} {10} {20}

结果就出来了...

7.2.代码

public static int[] fast_sort(int [] arr) {quick_sort(arr,0,arr.length-1);return arr;}public static void quick_sort(int [] arr,int l,int r) {if(l >= r) {return ;}int i = l;int j = r;int data = arr[l];while(i < j) {while(i < j && arr[j] > data) {j--;}while(i < j && arr[i] <= data) {i++;}if(i < j) {int tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;}}arr[l] = arr[i];arr[i] = data;
//到这儿 i之前的都小于基准值   i+1之后的都大于基准值quick_sort(arr,l,i-1);quick_sort(arr,i+1,r);}

8.堆排序

8.1.算法思想

首先介绍一下什么是堆？ 堆其实是一棵有带有某种顺序的完全二叉树。主要分为大顶堆和小顶堆，大顶堆代表的完全二叉树是：父节点上的值大于其左右子树的节点上的值：

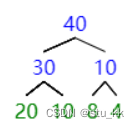
而小顶堆就是父节点的值小于左右子树节点上的值：

所以堆排序的原理就是将数组构建成一个大（小）顶堆，每次将根节点（根节点就是最大（小）值），取出之后，我们将剩下的数据继续进行构造大（小）顶堆。

接下来以大顶堆为例子，演示升序排序的过程，初始状态：（这里用数组代表完全二叉树，假设arr[x] 为父节点的话，左子节点为2*x+1 右子节点为2*x+2 。 如果x是从下标1开始，那么左子节点为2*x， 右子节点为2*x+1 。）如下图：我们的arr数组（小标从零开始）应该为{40，30，10，20，10，8，4}

1. 首先构造成功之后，我们将头节点取出，这里的操作是将它和最后一个数据(4)交换，这时候已经有序的是{40}。如图：

2. 接下来将完全二叉树继续进行大顶堆的构造：

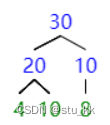
3. 构造成功之后，我们将头节点取出，这里的操作是将它和最后一个数据交换，这时候已经有序的是{30，40}。如图：

4. 接下来将完全二叉树继续进行大顶堆的构造：

5. 构造成功之后，我们将头节点取出，这里的操作是将它和最后一个数据交换，这时候已经有序的是{20，30，40}。如图：

6. 接下来继续将完全二叉树继续进行大顶堆的构造：

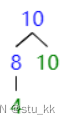
7. 构造成功之后，我们将头节点取出，这里的操作是将它和最后一个数据交换，这时候已经有序的是{10，20，30，40}。如图：

8. 接下来继续将完全二叉树继续进行大顶堆的构造：

9. 构造成功之后，我们将头节点取出，这里的操作是将它和最后一个数据交换，这时候已经有序的是{10 ，10，20，30，40}。如图：

10. 接下来继续将完全二叉树继续进行大顶堆的构造：

11. 构造成功之后，我们将头节点取出，这里的操作是将它和最后一个数据交换，这时候已经有序的是{8，10 ，10，20，30，40}。最后只剩下4,也就是最小的数了，将它放进去就好了。

12. 结果就是{4，8，10，10，20，30，40}

8.2.代码

    public static int[] heap_sort(int[]arr){int len = arr.length - 1;
//        TODO 从中间出发，因为 arr[x] 为父节点的话，左子节点为2*x+1 右子节点为2*x+2 所以最右边的父节点为( len -1 )/2
//        TODO 构建大顶堆for(int i = (len-1)/2; i >= 0; i--){HeapChange(arr,i,len);}for(int i = len;i > 0;i--){//TODO  因为大顶堆的根节点最大，交换第一个和最后一个的话，最大值就去到尾部啦，也就可以实现升序了int tmp = arr[0];arr[0] = arr[i];arr[i] = tmp;HeapChange(arr,0,i-1);}return arr;}private static void HeapChange(int[] arr, int start, int end) {int father = start; //TODO 父节点int son = father * 2 + 1; //TODO　左子节点//TODO 这里我们需要把左右子节点中最大的值和父节点相比，如果比父节点大，那么就要交换，这就是大顶堆啦while(son <= end){ //TODO　不能数组越界if(son <= end -1 && arr[son] < arr[son+1]){ //TODO 和右节点进行大小比较son++; //TODO　成为右子节点}if(arr[father] >= arr[son]){break; //如果已经是大顶堆了就不用麻烦了}else{ //交换int tmp = arr[father];arr[father] = arr[son];arr[son] = tmp;}father = son;son = father * 2 + 1;}}

9.计数排序

9.1.算法思想

计数排序的思想很简单，就是统计原数组中的每个数出现的次数，结果存放到统计数组中，然后从小到大遍历一遍统计数组，按照次数输出数值，就排序成功了。

比如{1，2，4，4，10，3，2} 这七个数 我们用统计数组num[]，统计一下：num[1] = 1,num[2] = 2,num[3] = 1,num[4] = 2,num[10] = 1,然后我们遍历num[i ---> 1-10]，如果num[i] > 0 就输出num[i]个i,也就是 1，2，2，3，4，4，10 这样就排序成功啦

9.2.代码

public static int[] count_sort(int[] arr){int max  = Integer.MIN_VALUE;int min = Integer.MAX_VALUE;for(int i = 0; i

10.基数排序

10.1.算法思想

基数排序是逐步将数组中的数字按照其个位、十位、百位...直到最大位0~9进行排序，最后得到的顺序结果。

比如上面的例子，我们每一步每一步的分析：

初始状态： {10，4，2，8，9，20}

首先按照个位排序 ；{10，20} {2} {4} {8} {9}

其次按照十位： {2} {4} {8} {9} {10 ，20}

结果出来了，就是 {2，4，8，9，10，20}

10.2.代码

    public static int[] radix_sort(int[] arr){ //基数排序int max = arr[0];for(int i = 1;i

11.总结

比较各大算法的时间复杂度、空间复杂度和稳定性

排序算法	时间复杂度	空间复杂度	稳定性
冒泡排序	O()	O(1)	稳定
选择排序	O()	O(1)	不稳定
插入排序	O()	O(1)	稳定
希尔排序	O()	O(1)	不稳定
归并排序	O(nlogn)	O(n)	稳定
快速排序	O(nlogn)	O(logn)	不稳定
堆排序	O(nlogn)	O(1)	不稳定
计数排序	O(n+k) 【k是计数素组的大小】	O(k)	稳定
基数排序	O(d(n+k)) 【 d是最大数的长度,k是进制哦，比如样例中的k就是10】	O(n+k)	稳定