报告

一、基本概念

决策树的定义：首先，决策树是一种有监督的分类算法——即给定X，Y值，构建X，Y的映射关系。不同于线性回归等是多项式，决策树是一种树形的结构，一般由根节点、父节点、子节点、叶子节点构成如图所示。父节点和子节点是相对的，子节点可以由父节点分裂而来，而子节点还能作为新的父节点继续分裂；根节点是没有父节点，即初始分裂节点，叶子节点是没有子节点的节点，为终节点。每一个分支代表着一个判断，每个叶子节点代表一种结果。

这是在已知各种情况的发生的概率的基础上，通过构建决策树来进行分析的一种方式。

预测方式：根据输入的样本X的特征属性和决策树的取值，将输入的X样本分配到某一个叶子节点中。将叶子节点中出现最多的Y值，作为输入的X样本的预测类别。

目的：最优的模型应该是：叶子节点中只包含一个类别的数据。

但是，事实是不可能将数据分的那么的纯，因此，需要“贪心”策略，力争在每次分割时都比上一次好一些，分的更纯一些。

• 决策树构建过程

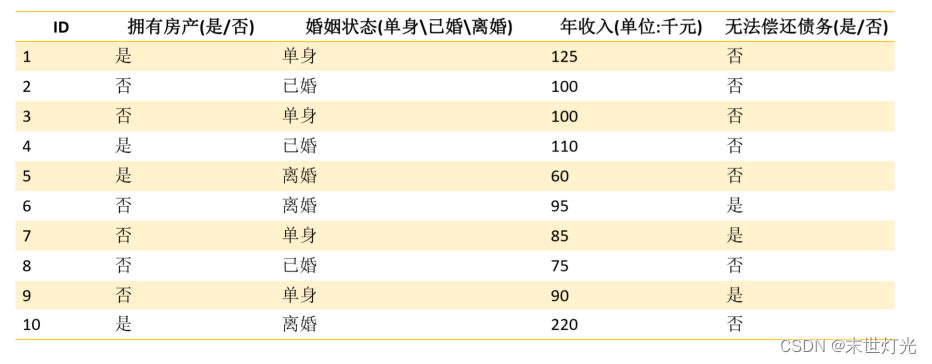
步骤一：将所有的特征看成一个一个的节点，eg（拥有房产、婚姻状态、年收入这些特征，我们可以看成一个一个的节点。）

步骤二：遍历当前特征的每一种分割方式，找到最好的分割点eg（婚姻状态这个特征，我们可以按照单身、已婚、离婚进行划分；也可以按照结过婚、没有结过婚进行划分）；将数据划分为不同的子节点，eg： N1、 N2….Nm；计算划分之后所有子节点的“纯度”信息

步骤三：使用第二步遍历所有特征，选择出最优的特征，以及该特征的最优的划分方式，得出最终的子节点N1、 N2….Nm

步骤四：对子节点N1、N2….Nm分别继续执行2-3步，直到每个最终的子节点都足够“纯”。

从上述步骤可以看出，决策生成过程中有两个重要的问题：

1. 对数据进行分割。
2. 选择分裂特征。
3. 什么时候停止分裂。

1. 对数据进行分割

根据属性值的类型进行划分：如果值为离散型，且不生成二叉决策树，则此时一个属性就是可以一个分支，比如：上图数据显示，婚姻状态为一个属性，而下面有三个值，单身、已婚、离婚，则这三个值都可以作为一个分类。如果值为离散型，且生成二叉决策树，可以按照 “属于此子集”和“不属于此子集”分成两个分支。还是像上面的婚姻状态，这可以按照已婚，和非婚，形成两个分支。如果值为连续性，可以确定一个值作为分裂点，按照大于分割点，小于或等于分割点生成两个分支，如上图数据，我可以按照6千元的点划分成：大于6千元和小于6千元。

2. 找到最好的分裂特征

决策树算法是一种“贪心”算法策略——只考虑在当前数据特征情况下的最好分割方式。在某种意义上的局部最优解，也就是说我只保证在当分裂的时候，能够保证数据最纯就好。对于整体的数据集而言：按照所有的特征属性进行划分操作，对所有划分操作的结果集的“纯度”进行比较，选择“纯度”越高的特征属性作为当前需要分割的数据集进行分割操作。

决策树使用信息增益作为选择特征的依据，公式如下：

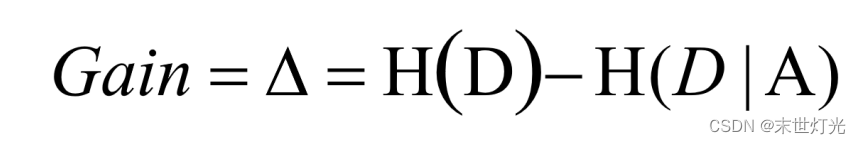
H（D）：分割前的纯度。

H（D｜A）：在给定条件A下的纯度，两者之差为信息增益度。如果信息增益度越大，则H（D｜A）越小，则代表结果集的数据越纯。

计算纯度的度量方式：Gini、信息熵、错误率。一般情况下，选择信息熵和Gini系数，这三者的值越大，表示越“不纯”。

Gini：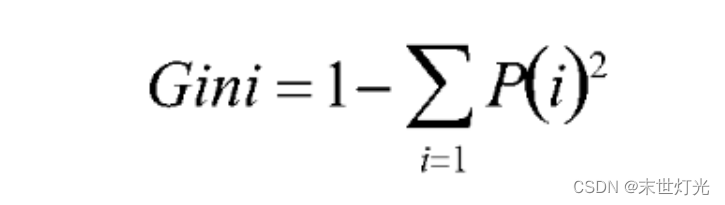

信息熵：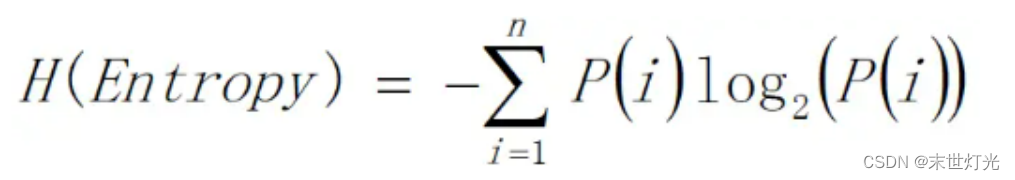

错误率：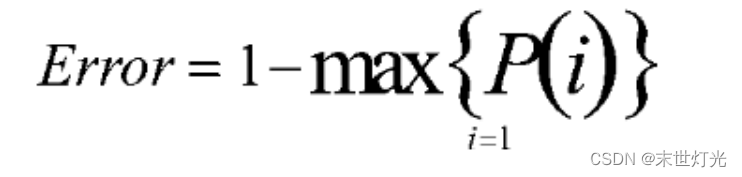

3. 什么时候停止分裂

一般情况有两种停止条件：当每个子节点只有一种类型的时候停止构建。当前节点中记录数小于某个阈值，同时迭代次数达到给定值时，停止构建过程。此时，使用 max(p(i))作为节点的对应类型。

方式一可能会使树的节点过多，导致过拟合(Overfiting)等问题。所以，比较常用的方式是使用方式二作为停止条件。

• ID3

ID3算法最早是由罗斯昆（J. Ross Quinlan）于1975年在悉尼大学提出的一种分类预测算法，算法以信息论为基础，其核心是“信息熵”。ID3算法通过计算每个属性的信息增益，认为信息增益高的是好属性，每次划分选取信息增益最高的属性为划分标准，重复这个过程，直至生成一个能完美分类训练样例的决策树。

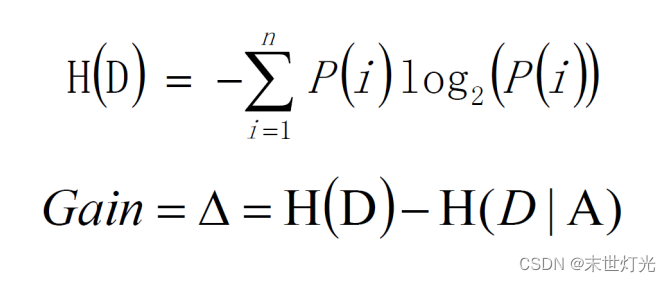
优点：决策树构建速度快；实现简单

缺点：

1.计算依赖于特征数目较多的特征，而属性值最多的属性并不一定最优 。

2.ID3算法不是递增算法，ID3算法是单变量决策树，对于特征属性之间的关系不会考虑。

3.抗噪性差。

4.只适合小规模数据集，需要将数据放到内存中。

代码：

import math
def splitDataSet(dataSet, i, value):'''返回数据集dataSet中，去掉第i列属性值为value的实例后形成的新的数据集'''retDataSet = []for x in dataSet:if x[i] == value:temp = x[:]temp.pop(i)retDataSet.append(temp)return retDataSetdef calcEntropy(dataSet):'''计算一个数据集的熵'''labelDict = {}  # 数据集的标签-该标签总个数for x in dataSet:label = x[-1]if label not in labelDict.keys():labelDict[label] = 0labelDict[label] += 1n = len(dataSet)retEntropy = 0.0for key in labelDict:p = float(labelDict[key]) / n  # 计算标签概率retEntropy -= p * math.log(p, 2)return retEntropydef calcInfoGain(dataSet, i):'''计算对数据集dataSet，选定第i列特征时所获得的信息增益'''preEntropy = calcEntropy(dataSet)postEntropy = 0.0featureSet = set([x[i] for x in dataSet])  # 得到i列特征所有特征值的集合for feature in featureSet:  # 以feature为筛选条件，计算筛选后的数据集熵subDataSet = splitDataSet(dataSet, i, feature)subDataSetEntropy = calcEntropy(subDataSet)p = len(subDataSet) / len(dataSet)postEntropy += p * subDataSetEntropyreturn preEntropy - postEntropydef getMaxInfoGainNode(dataSet, featureNameList):'''featureNameList是dataSet中各特征名称该函数返回两种结果：熵为0时，返回标签,类型为str熵不为0时，返回具有最大信息增益的特征的索引号，特征名，以及最大信息增益'''dataSetEntropy = calcEntropy(dataSet)if dataSetEntropy == 0:return dataSet[0][-1]  # 数据集熵为0，说明标签都相同，直接将该标签返回featureNum = len(featureNameList)maxInfoGain = 0maxInfoGainIndex = 0for i in range(0, featureNum):  # 遍历所有特征，获得具有最大信息增益的特征索引号infoGain = calcInfoGain(dataSet, i)if infoGain > maxInfoGain:maxInfoGain = infoGainmaxInfoGainIndex = ireturn maxInfoGainIndex, featureNameList[maxInfoGainIndex], maxInfoGaindef createID3Tree(dataSet, featureNameList):'''该函数返回一个结点如果dataSet熵为0，那么返回dataSet中类标签，此标签唯一否则，返回一个字典，该字典的key为dataSet选出的最优特征名，value又为一个字典，value字典的key为最优特征的特征值名，value字典的value又为一个字典.....'''maxInfoGainNode = getMaxInfoGainNode(dataSet, featureNameList)if type(maxInfoGainNode) == str:return maxInfoGainNodenodeIndex, nodeName = maxInfoGainNode[0], maxInfoGainNode[1]ret = {}ret[nodeName] = {}featureSet = set([x[nodeIndex] for x in dataSet])for feature in featureSet:subDataSet = splitDataSet(dataSet, nodeIndex, feature)newFeatNameList = featureNameList[:]newFeatNameList.pop(nodeIndex)childTree = createID3Tree(subDataSet, newFeatNameList)  # 对以最大信息增益作为特征筛选后的子数据集进行递归调用ret[nodeName][feature] = childTreereturn retdataSet = [['青年', '否', '否', '一般', '拒绝'],['青年', '否', '否', '好', '拒绝'],['青年', '是', '否', '好', '同意'],['青年', '是', '是', '一般', '同意'],['青年', '否', '否', '一般', '拒绝'],['中年', '否', '否', '一般', '拒绝'],['中年', '否', '否', '好', '拒绝'],['中年', '是', '是', '好', '同意'],['中年', '否', '是', '非常好', '同意'],['中年', '否', '是', '非常好', '同意'],['老年', '否', '是', '非常好', '同意'],['老年', '否', '是', '好', '同意'],['老年', '是', '否', '好', '同意'],['老年', '是', '否', '非常好', '同意'],['老年', '否', '否', '一般', '拒绝'], ]featureNameList = ['年龄', '有工作', '有房子', '信贷情况']
ID3Tree = createID3Tree(dataSet, featureNameList)
print("数据集1:",ID3Tree)
dataSet = [['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'],['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'],['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '好瓜'],['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘', '好瓜'],['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑', '好瓜'],['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜'],['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', '坏瓜'],['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑', '坏瓜'],['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘', '坏瓜'],['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑', '坏瓜'],['浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑', '坏瓜'],['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '坏瓜'],['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑', '坏瓜'],['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜']]
featureNameList = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感']
ID3Tree = createID3Tree(dataSet, featureNameList)
print("数据集2:",ID3Tree)
dataSet = [[1, 1, 1, 1, 'No'],[1, 1, 1, 2,  'No'],[2, 1, 1, 1,  'Yes'],[3, 2, 1, 1,  'Yes'],[3, 3, 2, 1,  'Yes'],[3, 3, 2, 2,  'No'],[2, 3, 2, 2,  'Yes'],[1, 2, 1, 1,  'No'],[1, 3, 2, 1,  'Yes'],[3, 2, 2, 1,  'Yes'],[1, 2, 2, 2,  'Yes'],[2, 2, 1, 2,  'Yes'],[2, 1, 2, 1,  'Yes'],[3, 2, 1, 2,  'No'], ]
featureNameList = ['outlook', 'temp', 'humidity', 'windy']ID3Tree = createID3Tree(dataSet, featureNameList)
print("数据集3:",ID3Tree)

运行结果：

• C4.5

在ID3算法的基础上，进行算法优化提出的一种算法(C4.5)，使用信息增益率来取代ID3中的信息增益。

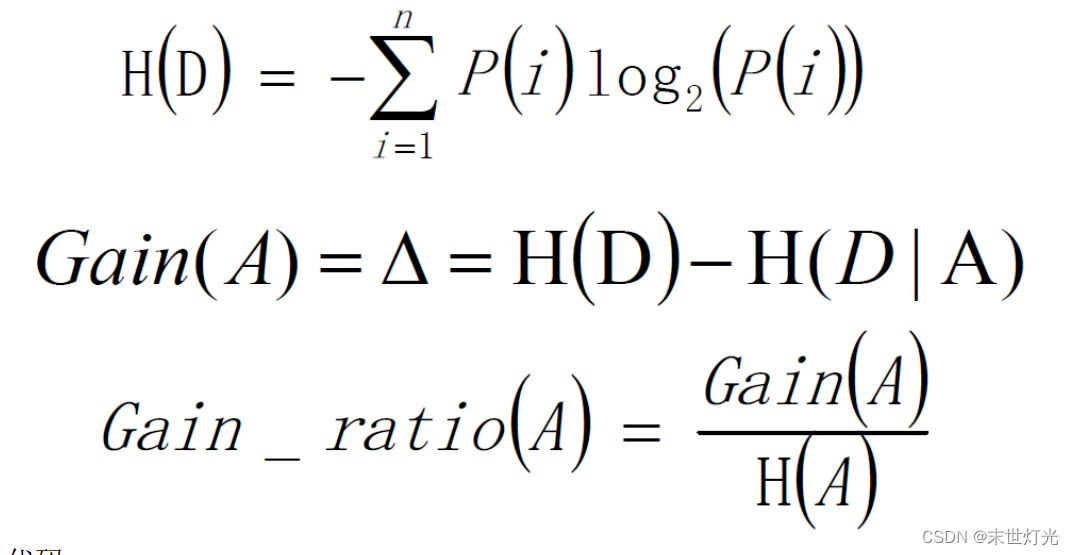
代码：

from math import log,sqrt

import operator
import redef classCount(dataSet):labelCount={}for one in dataSet:if one[-1] not in labelCount.keys():labelCount[one[-1]]=0labelCount[one[-1]]+=1return labelCountdef calcShannonEntropy(dataSet):labelCount=classCount(dataSet)numEntries=len(dataSet)Entropy=0.0for i in labelCount:prob=float(labelCount[i])/numEntriesEntropy-=prob*log(prob,2)return Entropydef majorityClass(dataSet):labelCount=classCount(dataSet)sortedLabelCount=sorted(labelCount.items(),key=operator.itemgetter(1),reverse=True)return sortedLabelCount[0][0]def splitDataSet(dataSet,i,value):subDataSet=[]for one in dataSet:if one[i]==value:reduceData=one[:i]reduceData.extend(one[i+1:])subDataSet.append(reduceData)return subDataSetdef splitContinuousDataSet(dataSet,i,value,direction):subDataSet=[]for one in dataSet:if direction==0:if one[i]>value:reduceData=one[:i]reduceData.extend(one[i+1:])subDataSet.append(reduceData)if direction==1:if one[i]<=value:reduceData=one[:i]reduceData.extend(one[i+1:])subDataSet.append(reduceData)return subDataSetdef chooseBestFeat(dataSet,labels):baseEntropy=calcShannonEntropy(dataSet)bestFeat=0baseGainRatio=-1numFeats=len(dataSet[0])-1bestSplitDic={}i=0# print('dataSet[0]:' + str(dataSet[0]))for i in range(numFeats):featVals=[example[i] for example in dataSet]#print('chooseBestFeat:'+str(i))if type(featVals[0]).__name__=='float' or type(featVals[0]).__name__=='int':j=0sortedFeatVals=sorted(featVals)splitList=[]for j in range(len(featVals)-1):splitList.append((sortedFeatVals[j]+sortedFeatVals[j+1])/2.0)for j in range(len(splitList)):newEntropy=0.0gainRatio=0.0splitInfo=0.0value=splitList[j]subDataSet0=splitContinuousDataSet(dataSet,i,value,0)subDataSet1=splitContinuousDataSet(dataSet,i,value,1)prob0=float(len(subDataSet0))/len(dataSet)newEntropy-=prob0*calcShannonEntropy(subDataSet0)prob1=float(len(subDataSet1))/len(dataSet)newEntropy-=prob1*calcShannonEntropy(subDataSet1)splitInfo-=prob0*log(prob0,2)splitInfo-=prob1*log(prob1,2)gainRatio=float(baseEntropy-newEntropy)/splitInfo# print('IVa '+str(j)+':'+str(splitInfo))if gainRatio>baseGainRatio:baseGainRatio=gainRatiobestSplit=jbestFeat=ibestSplitDic[labels[i]]=splitList[bestSplit]else:uniqueFeatVals=set(featVals)GainRatio=0.0splitInfo=0.0newEntropy=0.0for value in uniqueFeatVals:subDataSet=splitDataSet(dataSet,i,value)prob=float(len(subDataSet))/len(dataSet)splitInfo-=prob*log(prob,2)newEntropy-=prob*calcShannonEntropy(subDataSet)gainRatio=float(baseEntropy-newEntropy)/splitInfoif gainRatio > baseGainRatio:bestFeat = ibaseGainRatio = gainRatioif type(dataSet[0][bestFeat]).__name__=='float' or type(dataSet[0][bestFeat]).__name__=='int':bestFeatValue=bestSplitDic[labels[bestFeat]]##bestFeatValue=labels[bestFeat]+'<='+str(bestSplitValue)if type(dataSet[0][bestFeat]).__name__=='str':bestFeatValue=labels[bestFeat]return bestFeat,bestFeatValuedef createTree(dataSet,labels):classList=[example[-1] for example in dataSet]if len(set(classList))==1:return classList[0][0]if len(dataSet[0])==1:return majorityClass(dataSet)Entropy = calcShannonEntropy(dataSet)bestFeat,bestFeatLabel=chooseBestFeat(dataSet,labels)# print('bestFeat:'+str(bestFeat)+'--'+str(labels[bestFeat])+', bestFeatLabel:'+str(bestFeatLabel))myTree={labels[bestFeat]:{}}subLabels = labels[:bestFeat]subLabels.extend(labels[bestFeat+1:])# print('subLabels:'+str(subLabels))if type(dataSet[0][bestFeat]).__name__=='str':featVals = [example[bestFeat] for example in dataSet]uniqueVals = set(featVals)# print('uniqueVals:' + str(uniqueVals))for value in uniqueVals:reduceDataSet=splitDataSet(dataSet,bestFeat,value)# print('reduceDataSet:'+str(reduceDataSet))myTree[labels[bestFeat]][value]=createTree(reduceDataSet,subLabels)if type(dataSet[0][bestFeat]).__name__=='int' or type(dataSet[0][bestFeat]).__name__=='float':value=bestFeatLabelgreaterDataSet=splitContinuousDataSet(dataSet,bestFeat,value,0)smallerDataSet=splitContinuousDataSet(dataSet,bestFeat,value,1)# print('greaterDataset:' + str(greaterDataSet))# print('smallerDataSet:' + str(smallerDataSet))# print('== ' * len(dataSet[0]))myTree[labels[bestFeat]]['>' + str(value)] = createTree(greaterDataSet, subLabels)# print(myTree)# print('== ' * len(dataSet[0]))myTree[labels[bestFeat]]['<=' + str(value)] = createTree(smallerDataSet, subLabels)return myTreeif __name__ == '__main__':dataSet = [[1, '长', '粗', '男'],[2, '短', '粗', '男'],[3, '短', '粗', '男'],[4, '长', '细', '女'],[5, '短', '细', '女'],[6, '短', '粗', '女'],[7, '长', '粗', '女'],[8, '长', '粗', '女']]labels = ['序号', '头发', '声音']  # 两个特征print("数据集1",createTree(dataSet,labels))dataSet = [['青年', '否', '否', '一般', '拒绝'],['青年', '否', '否', '好', '拒绝'],['青年', '是', '否', '好', '同意'],['青年', '是', '是', '一般', '同意'],['青年', '否', '否', '一般', '拒绝'],['中年', '否', '否', '一般', '拒绝'],['中年', '否', '否', '好', '拒绝'],['中年', '是', '是', '好', '同意'],['中年', '否', '是', '非常好', '同意'],['中年', '否', '是', '非常好', '同意'],['老年', '否', '是', '非常好', '同意'],['老年', '否', '是', '好', '同意'],['老年', '是', '否', '好', '同意'],['老年', '是', '否', '非常好', '同意'],['老年', '否', '否', '一般', '拒绝'], ]labels = ['年龄', '有工作', '有房子', '信贷情况']print("数据集2", createTree(dataSet, labels))dataSet = [['Sunny', 'Hot', 'High', 'FALSE', 'N'],['Sunny', 'Hot', 'High', 'TRUE', 'N'],['Overcast', 'Hot', 'High', 'FALSE', 'P'],['Rain', 'Mild', 'High', 'FALSE', 'P'],['Rain', 'Cool', 'Normal', 'FALSE', 'P'],['Rain', 'Cool', 'Normal', 'TRUE', 'N'],['Overcast', 'Cool', 'Normal', 'TRUE', 'P'],['Sunny', 'Mild', 'High', 'FALSE', 'N'],['Sunny', 'Cool', 'Normal', 'FALSE', 'P'],['Rain', 'Mild', 'Normal', 'FALSE', 'P'],['Sunny', 'Mild', 'Normal', 'TRUE', 'P'],['Overcast', 'Mild', 'High', 'TRUE', 'P'],['Overcast', 'Hot', 'Normal', 'FALSE', 'P'],['Rain', 'Mild', 'High', 'TRUE', 'N']]labels = ['Outlook', 'Temperature', 'Humidity', 'Windy']print("数据集3", createTree(dataSet, labels))

运行结果：