1：概念

当数据有序，二叉搜索树将趋近于单叉树，查找元素相当于在顺序表中查找元素，效率低下，两位俄罗斯数学家G.M.Adelson-Velskii和E.M.Landis创建了AVL树。特性如下：

• 左右子树高度差的绝对值不超过1

• 左右子树都为AVL树

如果一棵树是高度平衡的，搜索效率就可以保持在log2的N

2：模拟实现

2.1：结构体定义

因为map/multimap/set/multiset底层是平衡搜索树，所以可以采用键值对插入的方式。

template
struct AVLTreeNode
{pair _kv;AVLTreeNode* left;AVLTreeNode* right;AVLTreeNode* parent;int _bf;AVLTreeNode(const pair& kv):left(nullptr),right(nullptr),parent(nullptr),_kv(kv),_bf(0){}
};

_bf是平衡因子，表示左右子树高度差。

2.2：平衡因子

平衡因子表示左右高度差，通常用右子树高度-左子树高度。

2.3：插入

插入就和二叉搜索树一样，用kv的键值对的K(first)比较，但是AVL树的插入分为2个步骤，插入节点和调整平衡因子。

    bool Insert(const pair& kv){if (_root == nullptr){_root = new Node(kv);}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first > kv.first){parent = cur;cur = cur->left;}else if (cur->_kv.first < kv.first){parent = cur;cur = cur->right;}else{return false;}}cur = new Node(kv);if (parent->_kv.first > kv.first){parent->left = cur;cur->parent = parent;}else{parent->right = cur;cur->parent = parent;}

先找到合适的位置，再判断自己是左节点还是右节点，将这个new的新节点和父亲链接起来。

2.3：调整平衡因子

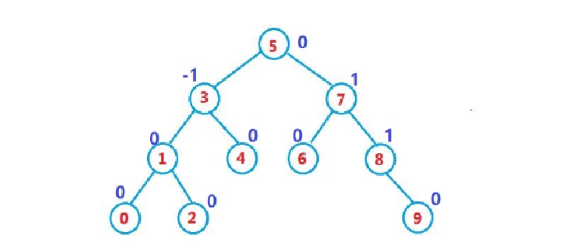
因为是插入孩子节点，所以要调整父亲的平衡因子，因此当父亲为空的时候停止调整。

           while(parent)if (cur = parent->left){parent->_bf--;}else{parent->_bf++;}

cur是左，平衡因子--，因为左高右低，同理反之。

因为AVL树要保持高度平衡，所以接下来要对父亲的平衡因子情况做判断。

            if (parent->_bf == 0){//没有高度变化break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->parent;}else if (parent->_bf == 2 || parent->_bf == -2){//旋转if (parent->_bf == 2 && cur->_bf == 1){//右子树高度发生了变化RotateR(parent);break;}}

• 如果父亲平衡因子变成0，说明原本是1或者-1，也就是从不平衡到平衡，这次插入是填充矮的一边，高度是不会发生变化的，不需要进行旋转。

• 如果父亲平衡因子变成了1的绝对值，说明从0到1和-1，（不可能从2变成1，从-2变成-1是因为插入的每一次要保证是AVL树，如果插入前已经不平衡，那么后续怎么旋转都没用），那么此时子树高度就发生了变化，变得更高了，但是如果是1的绝对值，还能满足AVL树的特性。

但是如图，9后再插入值，9的平衡因子变成了1，8的平衡因子变成了2，不能满足AVL树的特性了，所以当父亲的平衡因子变成1的绝对值的时候，表明parent所在子树的高度变化了，要持续向上更新。

• 当父亲的平衡因子变为2的绝对值，并且cur的平衡因子是1的时候，说明当前是在cur的右节点上插入了节点，导致高度严重不平衡。

2.3.1：左单旋

假设abc是高度为h的avl子树，因为之前说了cur的bf为1，说明是从c这里插入节点，c的高度变为h+1，此时就会发生左单旋，左单旋又分为多种情况。

2.3.1.1：h=0

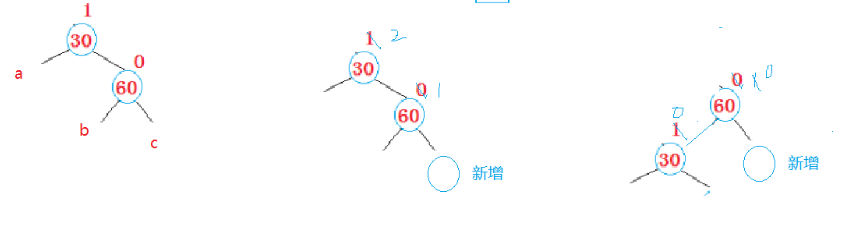
abc此时为空节点，将30链接到60的左孩子。

2.3.1.2：h=1

把b作为30的右孩子，30作为60的左孩子。因为b必然大于30小于60。30和a必然小于60。

c的左右新增都会引发旋转。

2.3.1.3：h=2

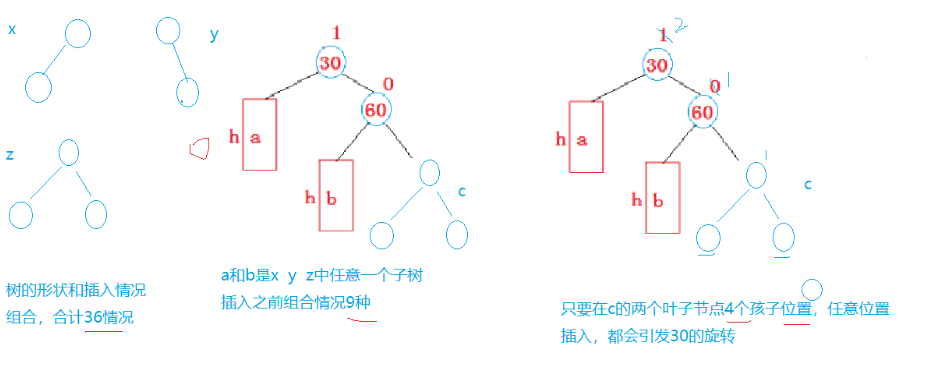
abc高度为2，那么a和b必然各自有3种情况，对于c肯定是z的形状，因为c插入了新节点导致c的高度变为了h+1，才会导致树不平衡，如果c是x或者y，插入了新节点后高度不会变，不会引发旋转。而且c如果是x或者y的情形，就等同于第一种情况h=0，因为我们这里所说的不同的h情况不只是针对整棵树，也有可能是部分的子树旋转。所以这里c如果是x或者y就和第一种情况一样。

所以c是z的形状，当c的2叶子节点的4个孩子节点任意位置插入1个节点，c的高度变为h+1，60的平衡因子变成1,30的平衡因子变成2，必然引发30的旋转。

2.3.1：左单旋实现

旋转的目的：

• 让左右子树高度差不超过1

• 旋转过程保证他是搜索树

• 更新调整孩子节点的平衡因子

• 保证子树的高度和插入前一致

    void RotateR(Node* parent){Node* subR = parent->right;Node* subRL = subR->left;parent->right = subRL;if (subRL){//不为空节点subRL->parent = parent;}Node* ppNode = parent->parent;subR->left = parent;parent->parent = subR;if (ppNode == nullptr){//更新root_root = subR;_root->parent = nullptr;}//parent不是根节点，说明还要把父亲和subr链接else{if (ppNode->left == parent){ppNode->left = subR;}else{ppNode->right = subR;}subR->parent = ppNode;}parent->_bf = subR->_bf = 0;}

因为结束条件是parent为空就停止调整，所以每次传parent给单旋函数。

实际上调整的是parent右节点/右节点的左节点/parent/parent的parent这4个节点的关系。

思路就是

• 定义2个指针指向parent的右和右的左

• parent的右指向subRL

• 当subRL不为空的时候，subRL的parent指向parent

• subR的左指向parent

• 定义指针指向parent的parent，因为不确定parent是否为根节点，如果不为根节点，因为parent的parent需要更改为subR，但是parent不是根节点，他还有parent，还应该把更改前的parent的parent与subR进行链接，否则找不到parent的parent。

• parent的parent指向subR

• 如果parent的parent是空，说明parent本来是根节点，此时就让根节点变成subR，并且让subR也就是root根节点的父亲变为空指针。不置空那么subR的父亲还仍然指向parent。

• 如果parent的parent不为空，说明parent不是根节点，此时判断parent是左还是右，然后对应着把parent的parent的左/右链接到subR，

• 把subR的父亲链接到ppnode

• 调整parent和subR的平衡因子(目的之一）

为什么旋转一次就可以break了？因为到了当前子树部分（也有可能到了根，不影响），因为当前子树部分的高度变化了，导致上面的高度也会变化，所以旋转当前部分的子树，子树的高度又变为插入之前一样的高度了，上面的高度又会恢复，所以旋转一次break就行。

2.3.2：右单旋

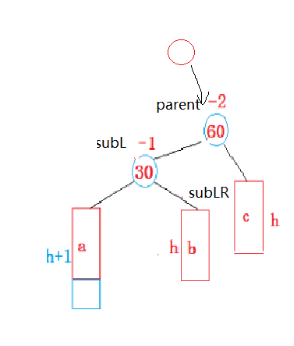
与单左旋差不多

    void RotateL(Node* parent){Node* subL = parent->left;Node* subLR = subL->right;parent->left = subLR;if (subLR){subLR->parent = parent;}Node* ppnode = parent->parent;parent->parent = subL;subL->right = parent;if (ppnode == nullptr){_root = subL;_root->parent = nullptr;}else{if (ppnode->left = parent){ppnode->left = subL;}else{ppnode->right = subL;}subL->parent = ppnode;}parent->_bf = subL->_bf = 0;}

2.3.3：双旋转

我们前面2种情况的插入是直着插入，如果是右边这种旋转的插入，就算是用前面的办法，把2的左边给1的右边，1作为3的左边，旋转后这样仍然是旋转的样子，不能让子树保持跟插入前的高度一致（就算不能让父亲重新回到0这个平衡因子）。

因此给出了方法，二次旋转。

针对这个又可以画图来分析一下什么情况会导致需要旋转

2.3.3.1：h=0

（此时bc的父亲节点相当于不存在）

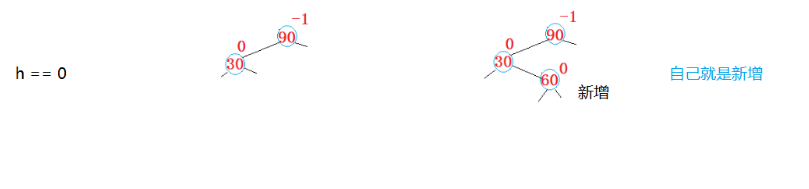
2.3.3.2：h=1

2.3.3.3：h=2

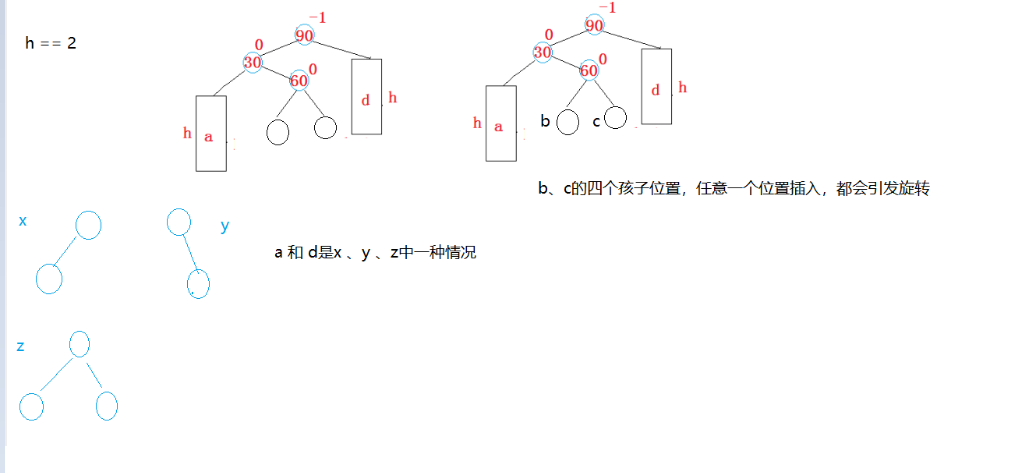
b和c必须为z才能导致插入后会发生旋转。

2.3.3.4：双旋过程

双旋情况：

parent和cur分别为-2,1或者2,-1

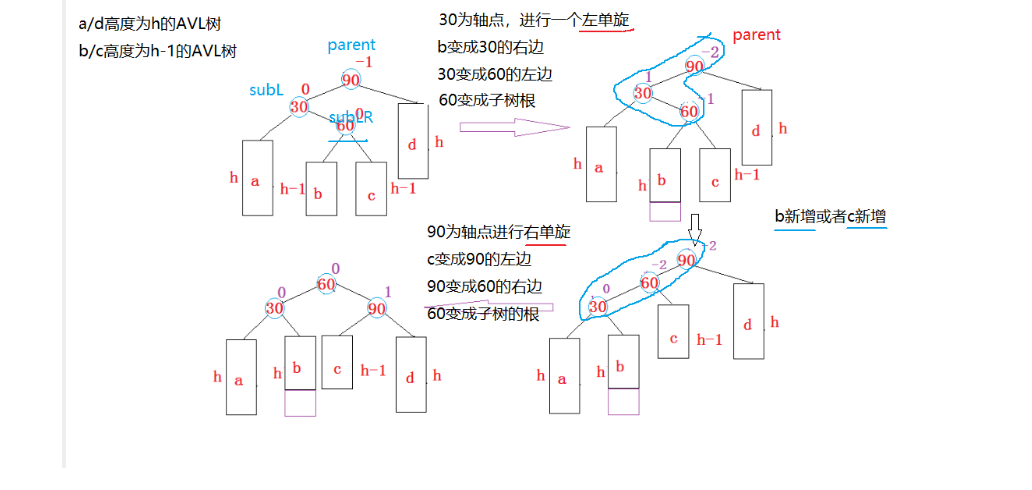
步骤：

• 先以30为父亲节点，此时90相当于ppnode，会用来进行链接60

• 然后以90为父亲节点，再进行右旋。

但是用代码复用的话，平衡因子更新有问题，左旋的话30和60的因子会变成0，右旋的话60和90的因子会变成0。

如果不从单旋分下来看这个问题，本质上这个问题就是把60的b拆分给30的右，60的c拆分给90的左，这样的话90的bf是1,30的bf才是0，更何况如果父亲的bf是-2&&cur的bf是1的时候，b和c哪个插入都不知道，这样一来b和c的平衡因子都不确定，明显平衡因子有错误。

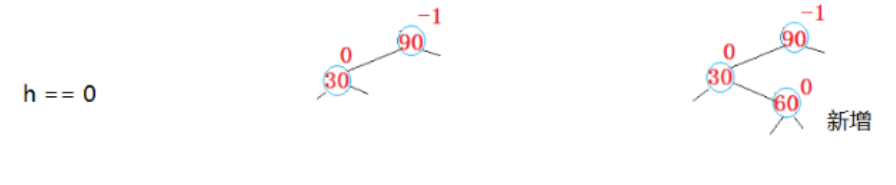
同样的，在h=0的时候，60就是新增，先进行左旋的话（以60为轴点），就是60的左边给30的右边，30变成60的左边，再以90为轴点右旋，就是60的右边变成90的左边，90变成60的右边。

2.3.3.5：双旋的平衡因子调整和双旋LR代码

因此可以根据60的平衡因子来判断是b插入还是c插入还是60就是新增，针对3个情况写出如下的代码。

    void RotateRL (Node* parent){Node* subL = parent->left;Node* subLR = subL->right;int bf = subLR->_bf;RotateL(parent->right);RotateL(parent);if (bf == -1){//sublr左边新增subL->_bf = 0;parent->_bf = 1;subLR->_bf = 0;}else if (bf == 1){//sublr右边新增parent->_bf = 0;subL->_bf = -1;subLR->_bf = 0;}else if(bf == 0){//sublr就是新增parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}else{assert(false);}}

2.3.3.6：RF双旋代码

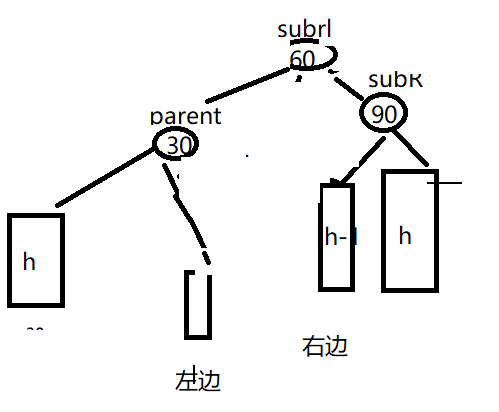
    void RotateRL(Node* parent){Node* subR = parent->right;Node* subRL = subL->left;int bf = subRL->_bf;RotateR(parent->right);RotateL(parent);if (bf == -1){//subrl左边新增subR->_bf = 1;parent->_bf = 0;subRL->_bf = 0;}else if (bf == 1){//subrl右边新增parent->_bf = -1;subR->_bf = 0;subRL->_bf = 0;}else if (bf == 0){//subrl就是新增parent->_bf = 0;subR->_bf = 0;subRL->_bf = 0;}else{assert(false);}}

注意pair的头文件包一下