题目描述

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。

图示两个链表在节点 c1 开始相交：

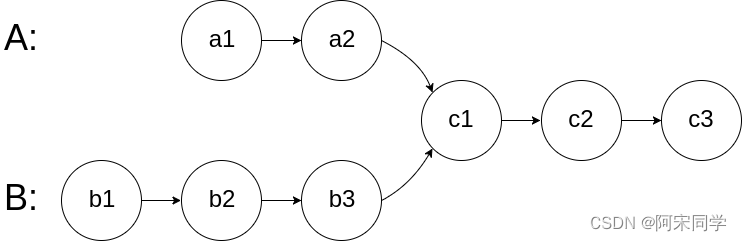
在这里插入图片描述

题目数据保证整个链式结构中不存在环。

注意，函数返回结果后，链表必须保持其原始结构。

示例 1：
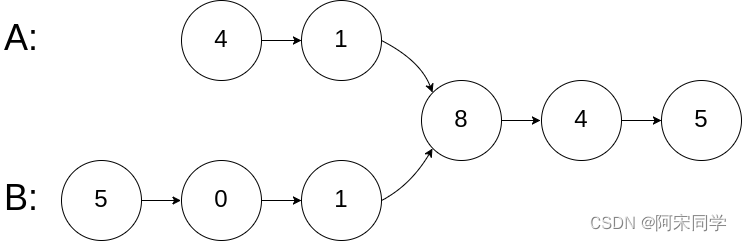
在这里插入图片描述

输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at ‘8’
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,0,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

示例 2：

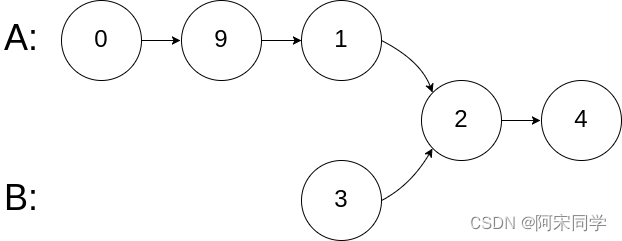
在这里插入图片描述

输入：intersectVal = 2, listA = [0,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1
输出：Intersected at ‘2’
解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [0,9,1,2,4]，链表 B 为 [3,2,4]。
在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

示例 3：
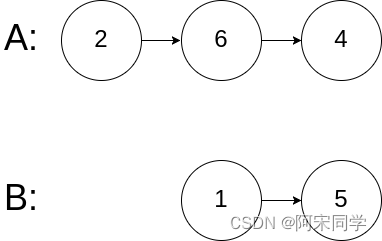
在这里插入图片描述

输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2
输出：null
解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。
由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。
这两个链表不相交，因此返回 null 。

提示：

listA 中节点数目为 m
listB 中节点数目为 n
0 <= m, n <= 3 * 104
1 <= Node.val <= 105
0 <= skipA <= m
0 <= skipB <= n
如果 listA 和 listB 没有交点，intersectVal 为 0
如果 listA 和 listB 有交点，intersectVal == listA[skipA + 1] == listB[skipB + 1]

进阶：你能否设计一个时间复杂度 O(n) 、仅用 O(1) 内存的解决方案？

解题思路与代码

哈希法

这道题我认为最简单易懂的就是哈希法，我们将headA的节点全部遍历进一个unordered_set中，然后再拿headB的节点一一去与存储在head中的节点去做对比，如果找到了，就直接返回。

简直太好懂了，之前我的思维一种困在如果对比节点数据相同的个数上，但节点数据相等不等于两个链表有相交的地方啊。看了哈希法后豁然开朗，直接对比节点就行了，下面请看代码：

class Solution {
public:ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {unordered_set set;ListNode* pos = headA;while(pos){set.insert(pos);pos = pos->next;}pos = headB;while(pos){if(set.count(pos)) return pos;pos = pos->next;}return nullptr;}
};

复杂度分析：
时间复杂度为O(m+n),其中m是链表headA的节点数，n是链表b的节点数，我们需要各遍历两个链表一次。
空间复杂度为O(m),其中m是链表headA的节点数，我们只需要将A的元素添加进集合即可

双指针法

题目开始的时候其实就已经明确的告诉过我们：保证题解中链表不会成环。所以不用去考虑链表成环问题。
这道题你仔细去看会发现一个规律，我们设置两个指针p1，p2，分别从链表headA，headB的开头开始遍历，p1遍历完a就去遍历b，同样p2遍历完b就去遍历a。如果，两个链表是相交的，则p1，p2，在变量的过程中，一定有一次会相等，反之，到变量结束都不相等。

这个规律你自己试一下就好了，不必去在乎数学的什么公式呀，其他的，心灵自然通畅，下面请看代码：

class Solution {
public:ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {ListNode* p1 = headA;ListNode* p2 = headB;while(p1 || p2){if(p1 == p2) return p1;if(!p1) p1 = headB;else p1 = p1->next;if(!p2) p2 = headA;else p2 = p2->next;}return nullptr;}
};

复杂度分析：
时间复杂度：O(m+n),m是链表A的节点个数，n是链表B的节点个数，我们需要遍历链表A，B各一次。
空间复杂度：O(1),我们没有使用额外的数据结构，只是设置了几个变量，所以是O(1)