leetcode_贪心算法
贪心算法相关题
- 简单题目
- 455.分发饼干
- 1005.K次取反后最大化的数组和
- 860.柠檬水找零
- 序列问题
- 376.摆动序列
- 法一:贪心法
- 法二:动态规划
- 单调递增的数字
- 简化版本
- 有点难度
- 53.最大子序和
- 贪心算法
- 动态规划
- 134.加油站
- 968.监控二叉树
- 两个维度权衡问题
- 分发糖果
- 406.根据身高重建队列
- 贪心解决股票问题
- 122.买卖股票的最佳时机II
- 贪心法
- 动规法
- 区间问题
- 55.跳跃游戏
- 贪心法
- 45.跳跃游戏II
- 动态规划
- 452.用最少数量的箭引爆气球
- 435.无重叠区间
- 736.划分字母区间
- 56.合并区间
- 补充(改版自弓箭数量那题)
- 贪心
简单题目
455.分发饼干
class Solution {
public:int findContentChildren(vector& g, vector& s) {sort(g.begin(),g.end());sort(s.begin(),s.end());int count=0,i=0,j=0;while(iif(s[j]>=g[i]) {count++;i++;}j++;}return count;}
};
1005.K次取反后最大化的数组和
class Solution {
public:static bool cmp(int a,int b){return abs(a)>abs(b);}int largestSumAfterKNegations(vector& nums, int k) {sort(nums.begin(),nums.end(),cmp);int sum=0;for(int i =0;iif(nums[i]<0&&k>0){nums[i] = -nums[i];k--;}}if(k%2==1) nums[nums.size()-1]*=-1;for(int i =0;isum+=nums[i];}return sum;}
};
860.柠檬水找零
class Solution {
public:bool lemonadeChange(vector& bills) {map map1;for(int i =0;iif(bills[i]==5)map1[5]++;if(bills[i]==10){map1[5]--;map1[10]++;if(map1[5]<0) return false;}if(bills[i]==20){if(map1[10]){map1[5]--;map1[10]--;}else{map1[5]-=3;}map1[20]++;if(map1[5]<0||map1[10]<0) return false;}} return true; }
};
序列问题
376.摆动序列
法一:贪心法
局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值
整体最优:整个序列有最多的局部峰值,从而达到最长摆动序列。
我们根据正常理解,可以总结出我们需要统计波动的数量,定义prediff(nums[i]-nums[i-1])和curdiff(nums[i+1]-nums[i]),则波动需要满足的条件是:(prediff<0&&curdiff>0) || (prediff>0&&curdiff<0)。
但是这样会忽略平坡的情况,平坡分两种,
-
一是上下坡中有平坡,对于这种情况,我们只统计一个波动就好,默认统计prediff=0的情况,就是平坡在前,上下坡在后,统计这一波动,这对应的也是代码随想录中提到的删除平坡中左面的元素。
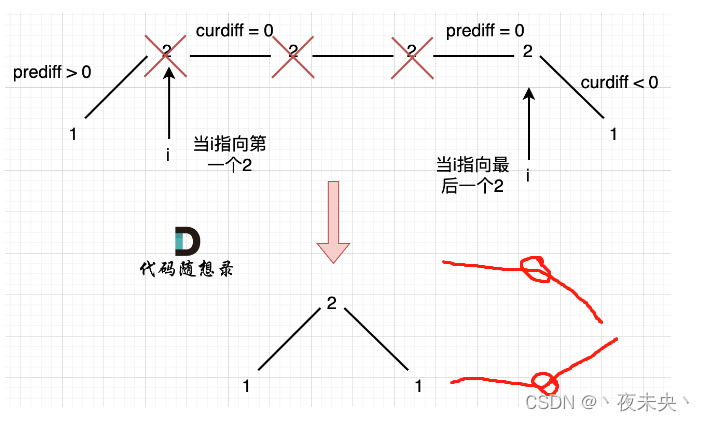
-
二是单调坡中有平坡,这对应的是我们应该修改对于prediff的更新,因为单调坡中的拐点使用上面的条件确实会被统计两次。
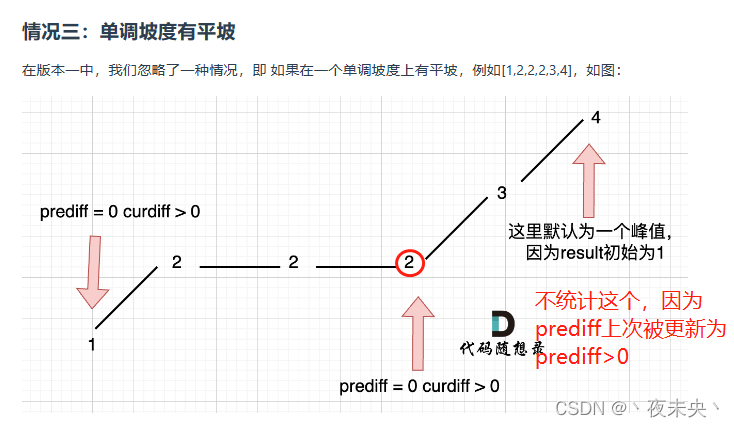
最后考虑两个数以及数组两端的情况,默认最右面有一个峰值(res=1起步),两个数的话无法判断写死摆动序列为2.
class Solution {
public:int wiggleMaxLength(vector& nums) {if(nums.size()==2) {if(nums[0]!=nums[1]) return nums.size();if(nums[0]==nums[1]) return 1;}int prediff=0,curdiff=0,res=1;for(int i =0;icurdiff=nums[i+1]-nums[i];if(prediff<=0&&curdiff>0||prediff>=0&&curdiff<0){res++;prediff=curdiff;}}return res;}
};
法二:动态规划
dp数组含义:
- dp[i][0]:表示考虑前i个数,第i个数作为山峰的摆动子序列最长长度
- dp[i][1]:表示考虑前i个数,第i个数作为山谷的摆动子序列最长长度
递推表达式:
dp[i][0] = max(dp[i][0],dp[j][1]+1) 其中0
class Solution {
public:int dp[1010][2];int wiggleMaxLength(vector& nums) {memset(dp,0,sizeof(dp));dp[0][0]=dp[0][1] = 1;for(int i =1;idp[i][0] = dp[i][1] = 1;for(int j =0;jnums[j]) dp[i][0] = max(dp[i][0],dp[j][1]+1);for(int j=0;j 单调递增的数字
class Solution {
public:int monotoneIncreasingDigits(int n) {if (n < 10) return n;string str = "";while (n) {char c = n % 10 + '0';str += c;n = n / 10;}reverse(str.begin(), str.end());for(int i =1;iif(str[i]str[i-1]-=1;for(int j=i;jstr[j]='9';}for(int k=i-2;k>=0;k--){if(str[k]>str[k+1]){str[k]-=1;str[k+1]='9';}}}}int num = 0;for (int i = 0; i < str.size(); i++) {num = num*10+str[i] - '0';}return num;}
};
简化版本
从后往前遍历,如果出现strNum[i - 1] > strNum[i]的情况,则strNum[i - 1]–,然后一直用一个flag记录i的位置,以便于之后将i之后所有卫生纸上的数字
class Solution {
public:int monotoneIncreasingDigits(int N) {string strNum = to_string(N);// flag用来标记赋值9从哪里开始// 设置为这个默认值,为了防止第二个for循环在flag没有被赋值的情况下执行int flag = strNum.size();for (int i = strNum.size() - 1; i > 0; i--) {if (strNum[i - 1] > strNum[i] ) {flag = i;strNum[i - 1]--;}}for (int i = flag; i < strNum.size(); i++) {strNum[i] = '9';}return stoi(strNum);}
};
有点难度
53.最大子序和
贪心算法
class Solution {
public:int maxSubArray(vector& nums) {int count=0,res=INT32_MIN;for(int i =0;icount+=nums[i];res = count>res?count:res;if(count<=0) count=0;}return res;}
};
动态规划
这道题写动规的时候,dp的含义直接设置成了前i个连续子数组的最大和,没有再设置res去保存最大值,导致dp[i]在更新的时候到底是最大值还是只是和的时候,出现了两层表示意义。比如1,2,3,-7,6,dp[3] = 6,但dp[3]按照原有含义,没有办法直接+nums[4]。
class Solution {
public:int dp[100010];int maxSubArray(vector& nums) {memset(dp,0,sizeof(dp));int res = nums[0];dp[0] = nums[0];for(int i =1;idp[i] = max(dp[i-1]+nums[i],nums[i]);if(dp[i]>res) res=dp[i];}return res;}
};
134.加油站
class Solution {
public:int canCompleteCircuit(vector& gas, vector& cost) {int min_gas = 0,sum_gas=0;for(int i =0;isum_gas=sum_gas+gas[i]-cost[i];if(sum_gassum_gas=0;for(int i=gas.size()-1;i>=0;i--){sum_gas+=gas[i]-cost[i];if(sum_gas>=-min_gas){return i;}}}return -1;}
};
968.监控二叉树
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:// 0:表示该节点没有被覆盖// 1:表示该节点有摄像头// 2:表示该节点被覆盖int ans;int traversal(TreeNode* cur){if(cur==nullptr) return 2;int left = traversal(cur->left);int right = traversal(cur->right);if(left==0||right==0) {ans++;return 1;}if(left==1||right==1){return 2;}if(left==2||right==2){return 0;}return -1;}int minCameraCover(TreeNode* root) {int root_num = traversal(root);if(root_num==0) ans++;return ans;}
};
两个维度权衡问题
分发糖果
class Solution {
public:int candy(vector& ratings) {vector candy(ratings.size(),1);for(int i=1;iif(ratings[i]>ratings[i-1]){candy[i] = candy[i-1]+1;}}for(int i=ratings.size()-1;i>0;i--){if(ratings[i-1]>ratings[i]){candy[i-1]=max(candy[i]+1,candy[i-1]);}}int ans=0;for(int i =0;ians+=candy[i];}return ans; }
};
406.根据身高重建队列
现根据身高从大到小排列,再根据k一个一个插入。
class Solution {
public:static bool cmp(vector& a,vector& b){if(a[0]==b[0]) return a[1]b[0];}vector> reconstructQueue(vector>& people) {sort(people.begin(),people.end(),cmp);vector> que;for(int i =0;iint position = people[i][1];que.insert(que.begin()+position,people[i]);}return que;}
};
贪心解决股票问题
122.买卖股票的最佳时机II
贪心法
class Solution {
public:int maxProfit(vector& prices) {int sum=0;for(int i =1;iif(prices[i]-prices[i-1]>0){sum+=prices[i]-prices[i-1];}}return sum;}
};
动规法
class Solution {
public:int dp[30010];int maxProfit(vector& prices) {memset(dp,0,sizeof(dp));int sum=0;for(int i =1;idp[i]=dp[i-1] + max(prices[i]-prices[i-1],0);}return dp[prices.size()-1];}
};
区间问题
区间问题总结,除了两个跳跃游戏。我们一共左了四个区间的贪心算法题。用最少弓箭射爆气球,五重叠区间的个数,划分字母区间和合并区间。用最少的弓箭射爆气球,实际上我们要找的是重叠区间的个数,而射爆气球这道题认为[1,2],[2,3]不属于重叠区间,这需要注意。我们按照左边界排序后,只需要遍历interval中每一个右边界,每次更新重叠区间的右端点r=min(points[i][1],r)r = \text {min}(\text{points}[i][1],r)r=min(points[i][1],r),然后处理每个interval左边界和r的关系就好。无重叠区间的个数实际上总区间个数减去重叠区间个数,所以看清楚条件[1,2],[2,3]属不属于重叠情况确立等号是否成立。划分字母区间这道题有点难度,需要统计每个字符出现的最远位置下标然后处理。合并区间,按左边界排序后,然后从左到右遍历看是否是重叠的,然后更新合并区间的左边界右边界。
55.跳跃游戏
贪心法
class Solution {
public:bool canJump(vector& nums) {int step=0;if(nums.size()==1) return true;for(int i =0;i<=step;i++){step=max(i+nums[i],step);if(step>=nums.size()-1) return true;}return false;}
};
45.跳跃游戏II
动态规划
class Solution {
public://我的思路是:dp数组表示到第i个格子需要的最短次数//dp数组更新的递推公式是:从j=0个格子开始找int dp[10100];int jump(vector& nums) {memset(dp, 10010, sizeof(dp));if (nums.size() == 1) return 0;else dp[0] = 0;for (int i = 1; i < nums.size(); i++) {for (int j = 0; j < i; j++) {if (j + nums[j] >= i) {dp[i] = min(dp[j] + 1, dp[i]);break;}}}return dp[nums.size() - 1];}
};
452.用最少数量的箭引爆气球
class Solution {
public:static bool cmp(vector& a, vector& b){if(a[0]==b[0]) return a[1]>& points) {sort(points.begin(),points.end(),cmp);int l=points[0][0],r=points[0][1];int ans=1;for(int i =1;il = points[i][0];r = min(points[i][1],r);if(l>r){r=points[i][1];ans++;}}return ans;}
};
435.无重叠区间
class Solution {
public://无重叠区间的个数等于总区间个数减去重叠区间个数static bool cmp(vector& a,vector& b){if(a[1]==b[1]) return a[0]>& intervals) {//这里需要记一下,按右边界排序要从左向右找//按左边界排序,要从右向左找sort(intervals.begin(),intervals.end(),cmp);int l=intervals[0][0],r=intervals[0][1];int ans=1;for(int i =1;iif(intervals[i][0]>=r){ans++;r=intervals[i][1];}}return intervals.size()-ans;}
};
736.划分字母区间
这道题不用回溯,不是所有的划分字母区间都要回溯,这道题主要在于统计之前遍历过所有字母的最远边界,如果当前下标到达了这个最远边界,说明到达了字符串的分割点。
class Solution {
public://贪心法map mp;vector ans;vector partitionLabels(string s) {for(int i =0;imp[s[i]] = i;}int split=0,split1=-1;for(int i =0;iif(mp[s[i]]>split) split=mp[s[i]];if(i==split){ans.push_back(split-split1);split1= split;} }return ans;}
};
56.合并区间
通过做这道题,我先是按照解上面题的常规套路,按照右边界排序,后来发现很多bug,这道合并区间的题如果从左到右遍历一定是先按左边界排列。
class Solution {
public:static bool cmp(vector&a, vector&b){if(a[0]==b[0]) return a[1]> res;vector> merge(vector>& intervals) {sort(intervals.begin(),intervals.end(),cmp);int l = intervals[0][0];int r = intervals[0][1];for(int i =1;iif(intervals[i][0]<=r){r = max(intervals[i][1],r);}else{res.push_back({l,r});l = intervals[i][0];r = intervals[i][1];}}res.push_back({l,r});return res;}
};
补充(改版自弓箭数量那题)
class Solution {
public://无重叠区间的个数等于总区间个数减去重叠区间个数static bool cmp(vector& a, vector& b){if(a[0]==b[0]) return a[1]>& intervals) {sort(intervals.begin(),intervals.end(),cmp);int l=intervals[0][0],r=intervals[0][1];int ans=1;for(int i =1;il = intervals[i][0];r = min(intervals[i][1],r);if(l>=r){ //加个等号,认为等于的情况不属于交叉区间r=intervals[i][1];ans++;}}return intervals.size()-ans;}
};
贪心
要从覆盖范围出发,不管怎么跳,覆盖范围一定是可以跳到的,以最小的步数增加覆盖范围,覆盖范围一旦覆盖了重点得到的就是最小步数。
class Solution {
public:int jump(vector& nums) {if(nums.size()==1) return 0;int curmaxindex = 0; // 当前覆盖最远距离下标,当前位置为i的话,能走到的最远距离就是i+nums[i]。int nextmaxindex = 0; // 记录走的最大步数int step = 0; // 下一步覆盖最远距离下标for(int i =0;i<=curmaxindex;i++){nextmaxindex = max(nums[i]+i,nextmaxindex); // 更新下一步能走到的最远距离if(i==curmaxindex){ // 如果i已经走到了当前能走到的最大距离if(curmaxindexstep++; // 那么我们一定要走下一步了,但下一步的落脚点在哪儿不用管// 不要误认为下一步落脚点一定是curdistance,这个没关系curmaxindex=nextmaxindex; // 更新当前覆盖最远距离下标if(nextmaxindex>=nums.size()-1) break; // 下一步的覆盖范围已经可以达到终点,结束循环}}}return step;}
};
上一篇:数据结构(一)(嵌入式学习)