实验二 离散控制系统的性能分析（时域/频域）

一、实验目的

1．掌握离散闭环系统的动态性能时域参数的分析与计算方法；

2．掌握离散系统稳定性的频域典型参数分析与计算方法。

二、实验工具

MATLAB 软件（ 2022a）；

三、实验内容

1．在 Matlab 语言平台上，通过给定的闭环离散系统，深刻理解时域参数的物理意义与计算方法，内容包括如下：

阻尼比参数分析：Z 平面与 S 平面的极点相互转换编程实现；分析 S/Z 两个平面域特殊特性（水平线、垂直线、斜线、圆周等）的极点轨迹相互映射方法；系统阶跃响应参数：上升时间和超调量等。

2． 采用频域分析方法，通过编程计算，进一步理解离散系统的稳定性参数，包括如下： 通过幅频图，进行增益裕度分析； 通过相频图，进行相位裕度分析。

四，实验步骤

1.阻尼比计算

1. %Example 1 Damping ratio computation   
2. ts=0.1;   
3. gp=tf(1,[1 1 0])   
4. gz=c2d(gp,ts,'zoh')   
5. kz=tf(5*[1,-0.9],[1 -0.7],ts);   
6. sys_ta=feedback(gz*kz,1,-1)   
7. p=pole(sys_ta)- 2 -   
8. radii=abs(p);   
9. angl=angle(p)   
10. damp(sys_ta)   
11. real_s=log(radii)/ts   
12. img_s=angl/ts   
13. zeta=cos(atan(-img_s./real_s))   
14. wn=sqrt(real_s.^2+img_s.^2) 

运行结果：

2.水平 S 平面线到 z 平面的映射

1. %Example 2 Mapping of horizontal s-plane line to z-plane   
2. xx=[0:0.05:1]'   
3. N=length(xx)   
4. s0=-xx*35;   
5. s=s0*[1 1 1 1 1]+j*ones(N,1)*[0,0.25,0.5,0.75,1]*pi/ts   
6. plot(real(s(:,1)),imag(s(:,1)),'-o',real(s(:,2)),imag(s(:,2)),'-s',...   
7. real(s(:,3)),imag(s(:,3)),'-^',real(s(:,4)),imag(s(:,4)),'-*',...   
8. real(s(:,5)),imag(s(:,5)),'-v'),sgrid   
9. z=exp(s*ts)   
10. plot(real(z(:,1)),imag(z(:,1)),'-o',real(z(:,2)),imag(z(:,2)),'-s',...   
11. real(z(:,3)),imag(z(:,3)),'-^',real(z(:,4)),imag(z(:,4)),'-*',...   
12. real(z(:,5)),imag(z(:,5)),'-v'),zgrid  

 

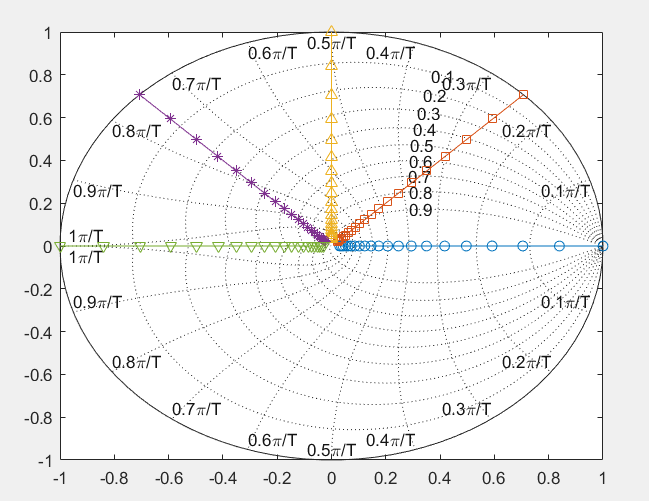
3.垂直 S 平面线到 z 平面的映射

1. %Example 3 Mapping of vertical s-plane line to z-plane  
2. s0=j*xx*pi/ts;   
3. s=ones(N,1)*[0,-5,-10,-20,-30]+s0*[1 1 1 1 1]   
4. plot(real(s(:,1)),imag(s(:,1)),'-o',real(s(:,2)),imag(s(:,2)),'-s',...   
5. real(s(:,3)),imag(s(:,3)),'-^',real(s(:,4)),imag(s(:,4)),'-*',...   
6. real(s(:,5)),imag(s(:,5)),'-v'),sgrid   
7. z=exp(s*ts)   
8. plot(real(z(:,1)),imag(z(:,1)),'-o',real(z(:,2)),imag(z(:,2)),'-s',...   
9. real(z(:,3)),imag(z(:,3)),'-^',real(z(:,4)),imag(z(:,4)),'-*',...   
10. real(z(:,5)),imag(z(:,5)),'-v'),zgrid 

4.恒定阻尼比 S 平面线映射到 z 平面

1. %Example 4 Mapping of constant damping ratio s-plane lines into z-plane   
2. s=s0*[1 1 1 1]-imag(s0)*[0,1/tan(67.5*pi/180),...   
3. 1/tan(45*pi/180),1/tan(22.5*pi/180)]   
4. s=[s,real(s(:,4))];   
5. plot(real(s(:,1)),imag(s(:,1)),'-o',real(s(:,2)),imag(s(:,2)),'-s',...   
6. real(s(:,3)),imag(s(:,3)),'-^',real(s(:,4)),imag(s(:,4)),'-*',...   
7. real(s(:,5)),imag(s(:,5)),'-v'),sgrid   
8. z=exp(s*ts)   
9. plot(real(z(:,1)),imag(z(:,1)),'-o',real(z(:,2)),imag(z(:,2)),'-s',...   
10. real(z(:,3)),imag(z(:,3)),'-^',real(z(:,4)),imag(z(:,4)),'-*',...   
11. real(z(:,5)),imag(z(:,5)),'-v'),zgrid  

5.将圆 s 平面线映射到 z 平面

1. %Example 5 Mapping of circle s-plane line to z-plane  
2. phi=xx*pi/2  
3. s0=(pi/ts)*(-cos(phi)+j*sin(phi))  
4. s=s0*[1,0.75,0.5,0.25,0]  
5. plot(real(s(:,1)),imag(s(:,1)),'-o',real(s(:,2)),imag(s(:,2)),'-s',...  
6. real(s(:,3)),imag(s(:,3)),'-^',real(s(:,4)),imag(s(:,4)),'-*',...  
7. real(s(:,5)),imag(s(:,5)),'-v'),sgrid  
8. z=exp(s*ts)  
9. plot(real(z(:,1)),imag(z(:,1)),'-o',real(z(:,2)),imag(z(:,2)),'-s',...  
10. real(z(:,3)),imag(z(:,3)),'-^',real(z(:,4)),imag(z(:,4)),'-*',...  
11. real(z(:,5)),imag(z(:,5)),'-v'),zgrid  

6.阶跃响应

1. %Example 6 Step response measure  
2. k=[0:1:60];  
3. step(sys_ta,k*ts);  

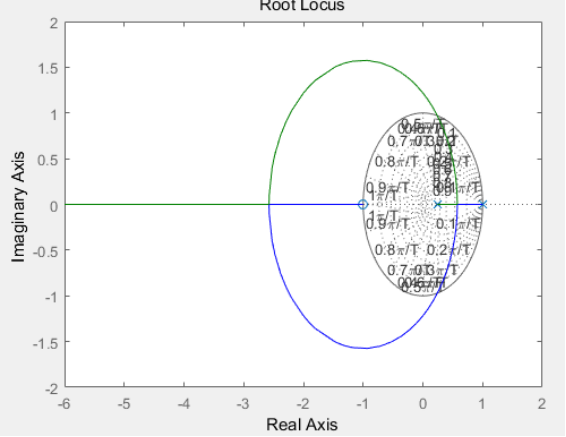
7.根轨迹

1. %Example 7 Root-locus analysis   
2. rlocus(gz*kz)   
3. Amplitude；  

1. %Example 8 Root-locus analysis in page 56   
2. numg=[1 0.5];   
3. deng=conv([1 -0.5 0],[1 -1 0.5]);   
4. sys_z=tf(numg,deng,-1)   
5. rlocus(sys_z)  

1. %Example 9 Root-locus analysis in page 57   
2. numg=[1];   
3. deng=[1 4 0];   
4. ts=0.25   
5. sys_s2=tf(numg,deng)   
6. sys_z2=c2d(sys_s2,ts,'imp')   
7. rlocus(sys_z2)   

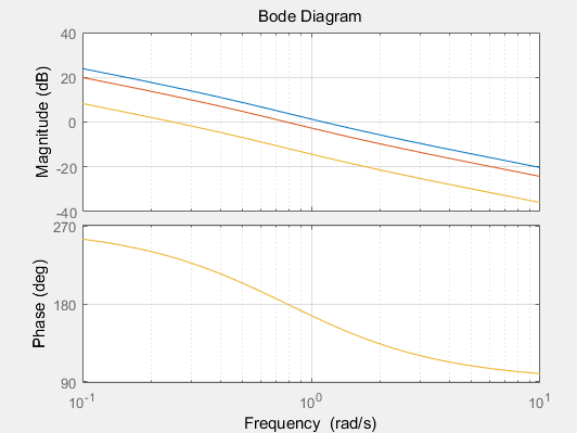
8.频率响应

1.     %Example 10 Analysis of frequency response and roots locus in page 59  
2. a=1.583e-7;  
3. k=[1e7,6.32e6,1.65e6];  
4. w1=-1;  
5. w2=1;  
6. ts=0.1;  
7. v=logspace(w1,w2,100);  
8. deng=[1.638 1 0];  
9. numg1=k(1,1)*a*[-1 1]  
10. numg2=k(1,2)*a*[-1 1]  
11. numg3=k(1,3)*a*[-1 1]  
12. sys_s1=tf(numg1,deng)  
13. sys_s2=tf(numg2,deng)  
14. sys_s3=tf(numg3,deng)  
15. bode(sys_s1,sys_s2,sys_s3,v),grid on 

1. numg=1.2e-7*[1 1]   
2. deng=conv([1 -1],[1 -0.242]);   
3. sys_z2=tf(numg,deng,ts)   
4. rlocus(sys_z2),grid on   

 五， 实验思考

1. S 平面与 Z 平面不同位置的映射关系分析

s平面虚轴的映射

s平面整个虚轴映射为z平面单位圆，左半平面任一点映射在z平面单位圆

内，右半平面任一点映射在单位圆外。

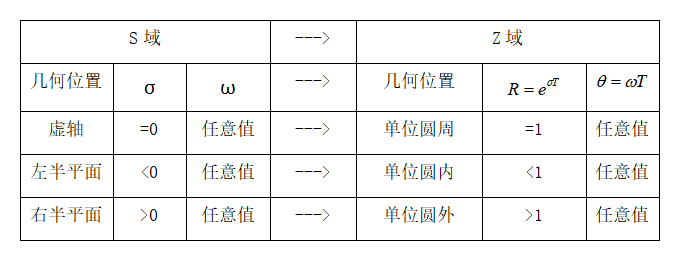
角频率ω与Z平面相角关系

2.离散系统根轨迹分析

Z平面上的根轨迹,是控制系统开环Z传递函数中的某个参数(如放大系数)连续变化时,闭环z传递函数的极点连续变化的轨迹。用根轨迹法分析系统闭环稳定性,不但可以知道在某个确定参数K下的稳定性,而且可以知道闭环极点的具体位置,尤其是K变化时的极点变化趋势,因此用它来指导参数整定是很直观的。具体画法与S域根轨迹方法一样。

3.离散系统 Bode 图分析

离散系统的的Bode 图也是分析离散系统的一种方法，可以通过截止频率，相角裕度，幅值裕度等观测系统的稳定性，为在频域中了解离散系统提供了有效的工具。

4.对离散系统相对稳定性的进一步思考。

离散稳定性的充分必要条件是：线性连续系统的稳定的充要条件是特征方程的根全部位于左半s平面。在离散系统中，根据s平面与z平面之间的映射关系：s = j ω , z = e j ω T ， 可以知道离散系统中的稳定域为以原点为圆心的单位原内。

我们知道，连续系统的劳斯——胡尔维茨稳定判据，是通过系统特征方程的系数及其符号来判断系统的稳定性。这个方法实际上仍是判断特征方程的根是否都在s平面的左半部。

然而，在离散系统中,判断系统的稳定性,是判断系统特征方程的根是否全在z平面的单位圆内。因此,离散系统不能直接应用劳斯——胡尔维茨判据来分析稳定性。从理论上分析，利用关系式z=exp(Ts)，可以将z为变量的特征方程转换为以s为变量的特征方程。

但因为s在指数中，代换运算不方便。为此，必须引入另一种线性变换。将z平面单位圆内区域映射为另一平面上的左半部。这样，就可以应用劳斯-胡尔维茨稳定判据米判断离散系统的稳定性。

为此，可采用双线性变换方法进行判断，即Z=(1+w)/(1-w)。采用修正劳斯——霍尔维茨判据的优点是把离散系统和连续系统的稳定性判据联系起来了。把z平面变换为w平面的另一好处是可以采用分析连续系统的频率法。但每种方法都存在缺点，他的缺点是要进行w变换，对于高阶系统，这种变换是比较麻烦的。