目录

1. 一维差分

 2.1 一维差分数组的构造（不重要）

2.2 一维差分数组的用途

 3. 二维差分

 3.1 二维差分的用途

1. 一维差分

差分与前缀和就可以理解成数学中微分与积分的关系，差分是前缀和的逆运算。

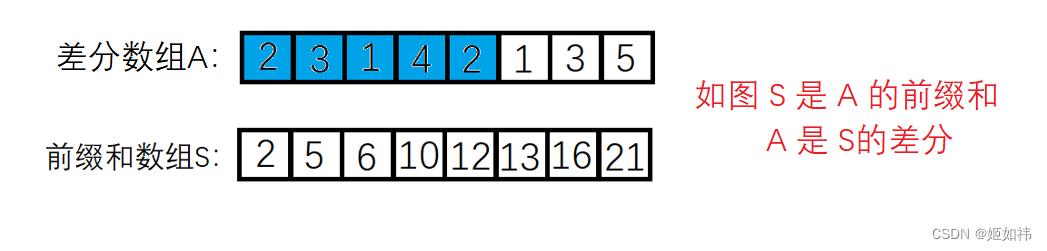
例如给定数组 A ，他的前缀和数组为 S，那么称 S 为 A 的前缀和，称 A 为 S 的差分。

 2.1 一维差分数组的构造（不重要）

有了前缀和数组我们就要想办法构造差分数组了，在数学上根据递推公式：An = Sn - S(n - 1)，其中 A 为差分数组，S为前缀和数组。这个公式并不重要哈，因为知道了差分数组的用途我们就可以很轻松地利用前缀和数组推导出差分数组。

2.2 一维差分数组的用途

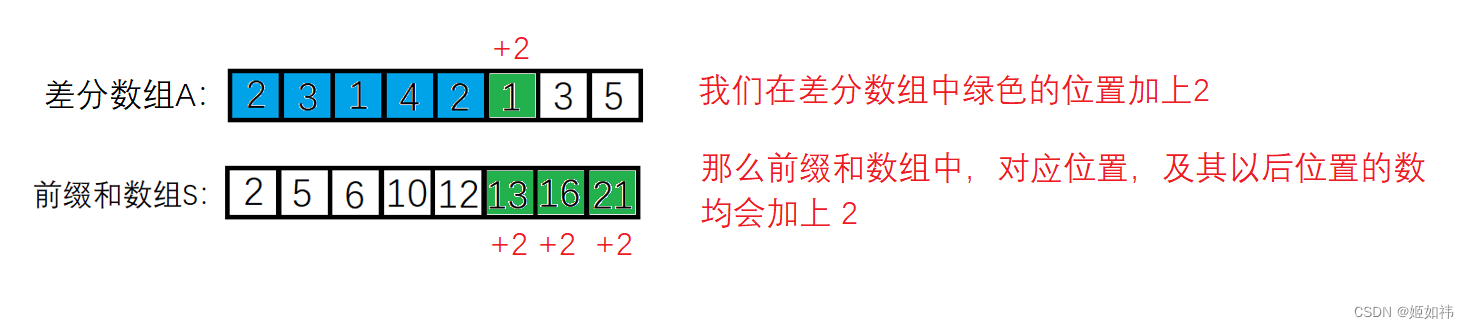
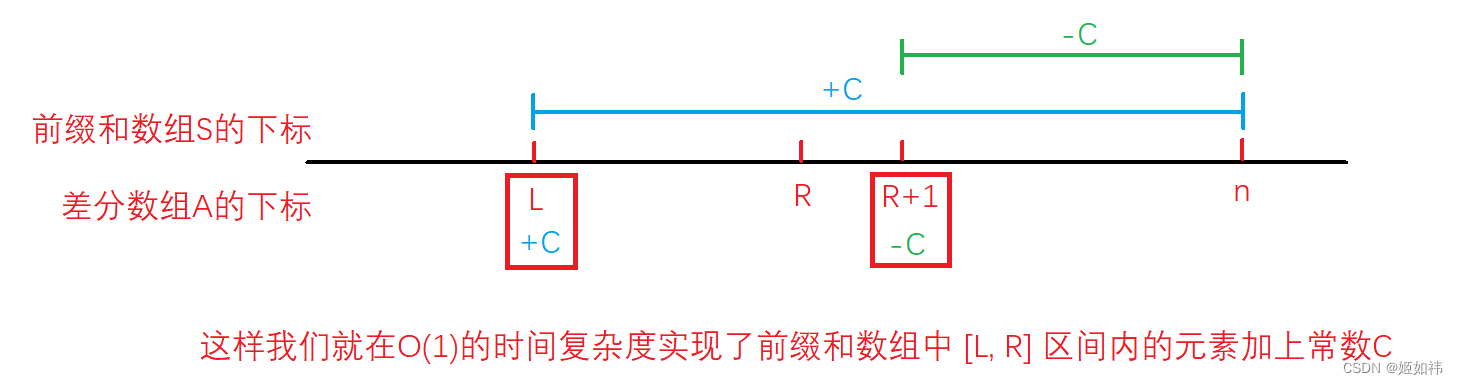
利用差分可以实现对前缀和数组中的一段区间的元素均加上常数 C 。例如：给定前缀和数组 S，S的差分数组 A ，现在我们要将前缀和数组 S 中 [ l, r ] 区间的所有元素加上常数 C，用循环显然需要O(N)的时间复杂度。但是如果我们求出来前缀和数组 S 的差分数组 A，那么我们就可以在差分数组中让 A[ l ] + C，同时让 A[ r + 1 ] - C，此时的差分数组对应的前缀和数组即是目标数组。这样我们就在 O(1) 的时间复杂度里面达到了想要的结果。

原理：根据前缀和数组的定义，当我们在差分数组的某一项加上一个常数 C 时，那么前缀和数组中的对应位置，及其以后位置的数均会加上常数 C。

当然想要前缀和数组中的某一个区间减去常数 C 也是一样的道理。现在我们就能够理解如何实现我们的要求了。

前面的 2.1 说了那种差分数组的构造方法并不重要。这是因为我们弄清楚了利用差分数组能够在前缀和数组中使得 [ l, r ] 区间内的元素加上常数 C，我们就能够轻而易举地通过前缀和数组推出差分数组。

假设我们要求前缀和数组 S 的差分数组，我们构造一个前缀和数组 S1 假设每一个元素均为 0 ，那么前缀和数组 S1 对应的差分数组 A1 的每一个元素也是 0，这个时候我们用变量 i 访问前缀和数组 S 中的每一个元素（遍历），假设每次遍历得到的数为 C，那么我们可以把 C 看作是让前缀和数组 S1 区间为 [ i, i ] 内的元素加上 C，然后用上面介绍的方法即可推出 S 的差分数组。

 我们现在就可以尝试写代码啦。

输入长度为n的整数序列

接下来输入m个操作，每个操作包含三个整数 l，r，c，表示将序列中 [ l, r ] 之间的每个数加上c。

输入格式

第一行包含两个整数n和m。

第二行包含n个这个数，表示整数序列。

接下来m行，每行包括三个整数 l，r，c，表示一个操作

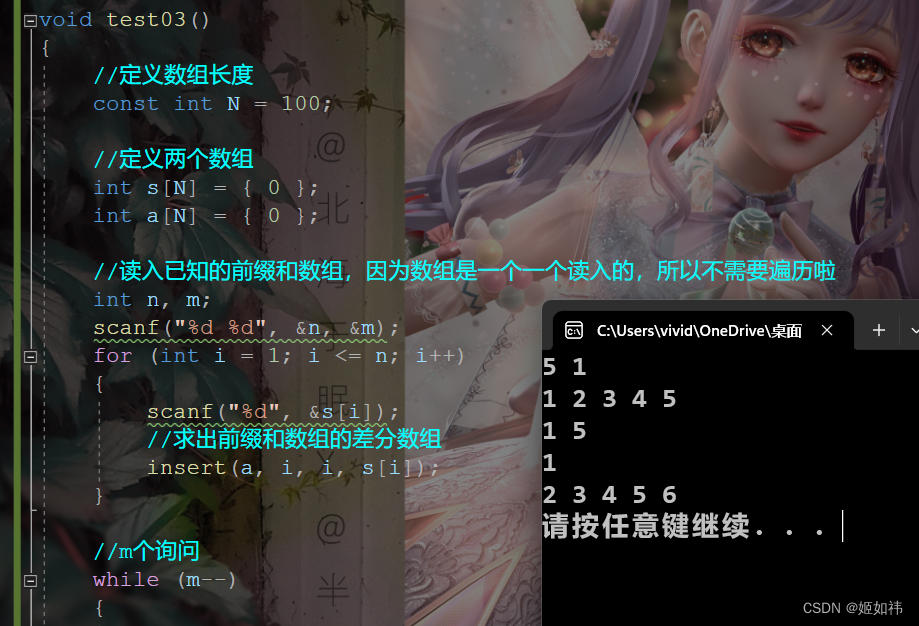
void test03()
{//定义数组长度const int N = 100;//定义两个数组int s[N] = { 0 };int a[N] = { 0 };//读入已知的前缀和数组，因为数组是一个一个读入的，所以不需要遍历啦int n, m;scanf("%d %d", &n, &m);for (int i = 1; i <= n; i++){scanf("%d", &s[i]);//求出前缀和数组的差分数组insert(a, i, i, s[i]);}//m个询问while (m--){int l, r, c;scanf("%d %d %d", &l, &r, &c);//前缀和数组的[l，r]区间加上cinsert(a, l, r, c);}//利用新的差分数组打印前缀和for (int i = 1; i <= n; i++){//递推求出新的差分数组的前缀和a[i] += a[i - 1];printf("%d ", a[i]);}printf("\n");
}int main()
{//一维差分test03();system("pause");return 0;
}

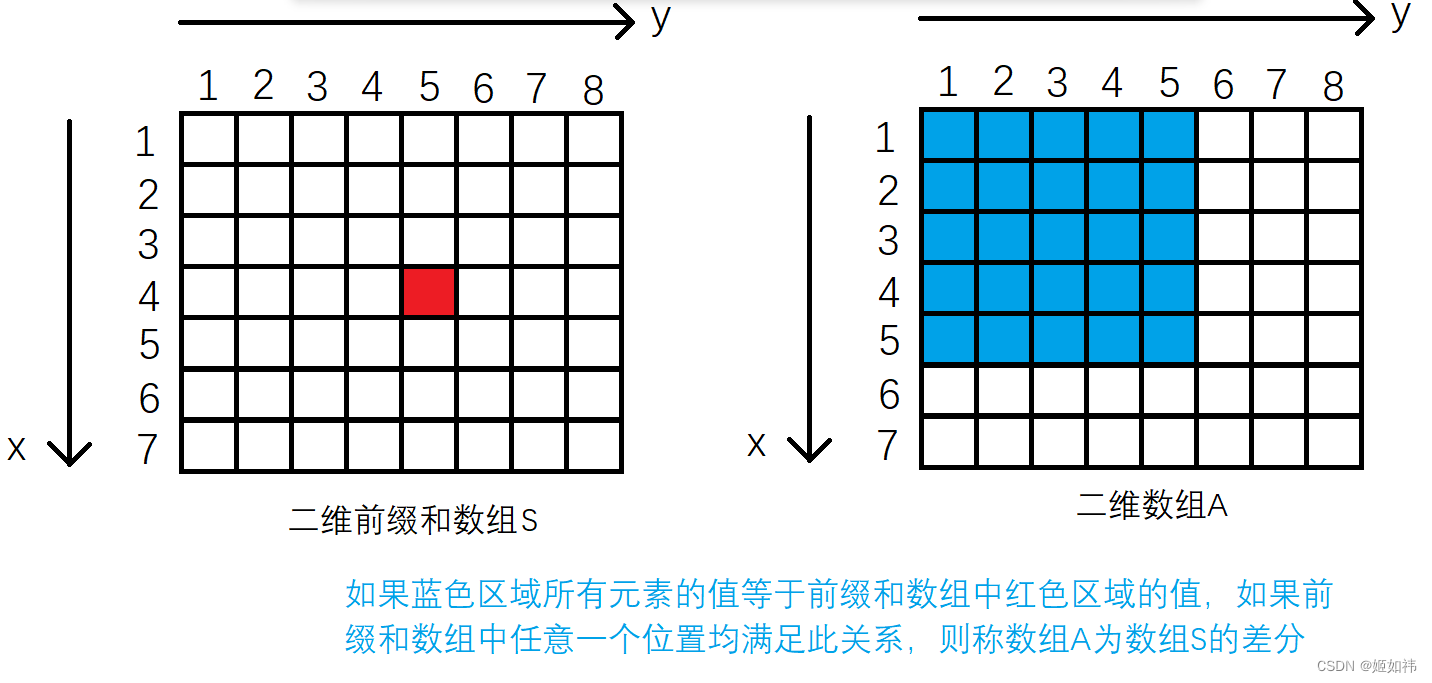
 3. 二维差分

二维差分：给定一个二维前缀和数组S，存在一个二维数组（矩阵）A，如果二维前缀和数组（矩阵）中 S[ i ][ j ] （i >= 1，i <= n）位置的元素满足：( A[1][1] + A[1][2] + ··· + A[1][j] ) + ( A[2][1] +

A[2][2] + ··· + A[2][j] ) + ··· + ( A[i][1] + A[i][2] + ··· + A[i][j] )。则称二维数组A为二维前缀和数组的差分数组。

 3.1 二维差分的用途

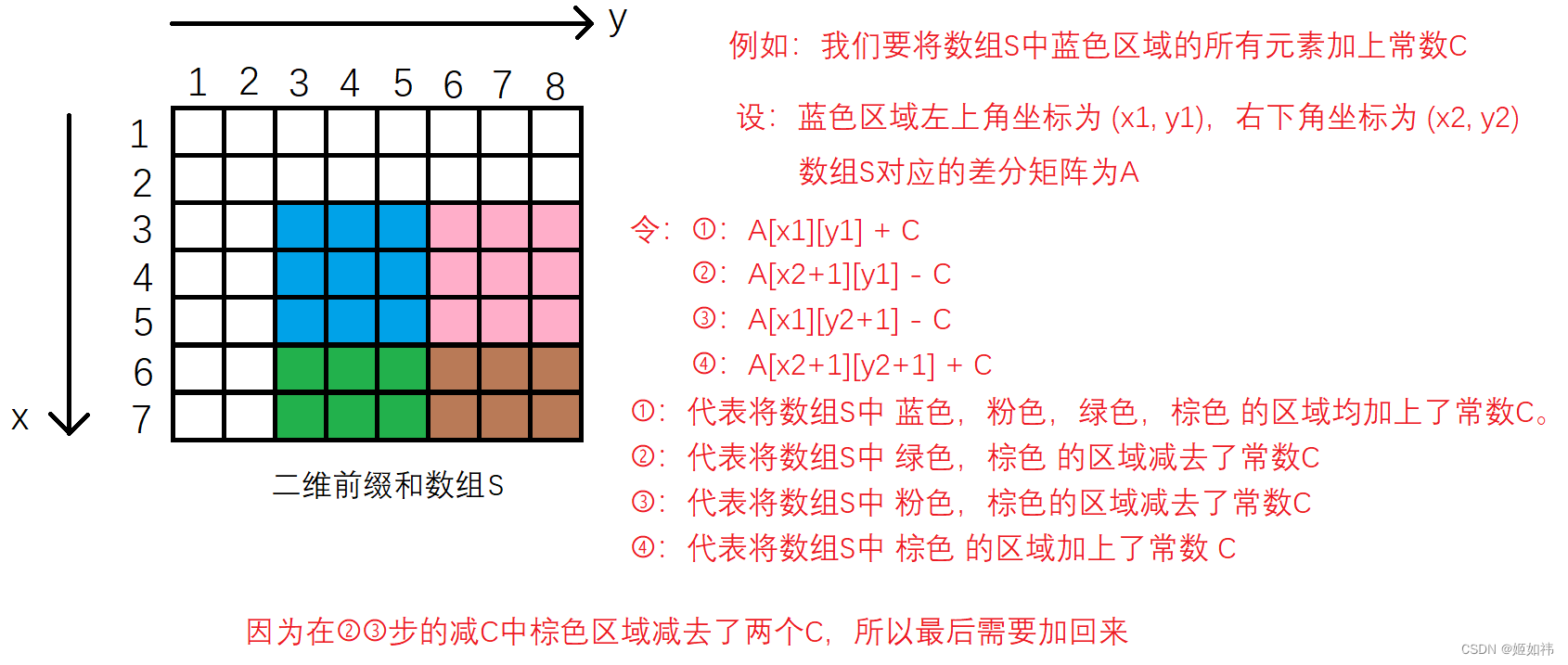
和一维差分的作用类似，只不过是使前缀和矩阵中某个子矩阵的所有元素加上常数C。方法如下：

在求出前缀和矩阵的差分矩阵后，要求我们让前缀和矩阵S中左上角坐标为 x1，y1；右下角坐标为x2，y2所围成的矩形里面的元素加上常数C。则只需要在差分矩阵A中，令A[x1][y1] + C，再令

A[x2+1][y1] - C，再令 A[x1][y2+1] - C，最后令 A[x2+1][y2+1] + C。这样我们就能够使前缀和矩阵中的某一子矩阵加上常数C啦。

 现在的问题就是怎么根据前缀和矩阵求出差分矩阵，原理和怎么求一维差分的数组是一样的。给定一个前缀和矩阵S，我们要求S的差分矩阵，首先构造一个前缀和矩阵S1，全部初始化为0，构造一个差分矩阵A全部初始化为0，此时A当然是S1的差分矩阵。然后我们利用 i，j 遍历给定的前缀和矩阵S，将遍历得到的结果 C 看作是在左上角坐标为 (i, j) ，右下角坐标为 (i, j) 的矩阵中加上常数C。通过上面的方法，以此类推，就可以得到前缀和矩阵S的差分矩阵啦。这里就不画图了。图与一维差分数组的求解差不多的。

下面我们就可以尝试写代码啦。

输入一个n行m列的整数矩阵，再输入q个操作，每个操作包含五个整数x1，y1，x2，y2，c，其中 (x1，y1)，(x2，y2) 分别表示子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素加上常数C。最后输出操作后的矩阵。

输入格式

第一行包含整数n，m，q。

接下来n行，每行包含m个整数，表示整数矩阵。

接下来q行，每行包含5个整数x1，y1，x2，y2，c，表示一个操作。

//定义数组的大小
const int N = 10;//将左上角坐标为(x1,y1),右下角坐标为(x2，y2)围成的矩阵中的元素加上c
void insert01(int(*a)[N], int x1, int y1, int x2, int y2, int c)
{a[x1][y1] += c;a[x1][y2 + 1] -= c;a[x2 + 1][y1] -= c;a[x2 + 1][y2 + 1] += c;
}void test04()
{//差分矩阵，前缀和矩阵均需要初始化为0int s[N][N] = { 0 };int a[N][N] = { 0 };int n, m, q;scanf("%d %d %d", &n, &m, &q);//读入前缀和矩阵for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){scanf("%d", &s[i][j]);//读入前缀和矩阵的同时求出对应的差分矩阵insert01(a, i, j, i, j, s[i][j]);}}//q个询问while (q--){int x1, x2, y1, y2, c;scanf("%d %d %d %d %d", &x1, &y1, &x2, &y2, &c);//对前缀和矩阵中的子矩阵加上常数cinsert01(a, x1, y1, x2, y2, c);}//利用递推关系求出新的差分矩阵对应的前缀和矩阵//这里是直接在差分矩阵上修改得到新的前缀和矩阵for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){a[i][j] += a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];printf("%d ", a[i][j]);}printf("\n");}printf("\n");
}int main()
{//二维差分test04();return 0;
}