目录

• 什么是斐波那契数列
• 递归写法
• • 使用递归写法的缺点
• 迭代写法(效率高)

什么是斐波那契数列

斐波那契数列（Fibonacci sequence），又称黄金分割数列，因数学家莱昂纳多·斐波那契（Leonardo Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、3

通俗地来讲，斐波那契数列就是从第三位数字开始，每位的值是其前两位的和

递归写法

使用递归方法写十分简单
从第三位数字开始，每位的值是其前两位的和

• f(0) = 1
• f(1) = 1
• f(n) = f(n-1)+f(n-2)(n>3)

代码如下：

long long feibonahi(int n)
{if (n <= 2){return 1;}else{return feibonahi(n - 1) + feibonahi(n - 2);}
}

使用递归写法的缺点

我们分析一下递归算法的时间复杂度

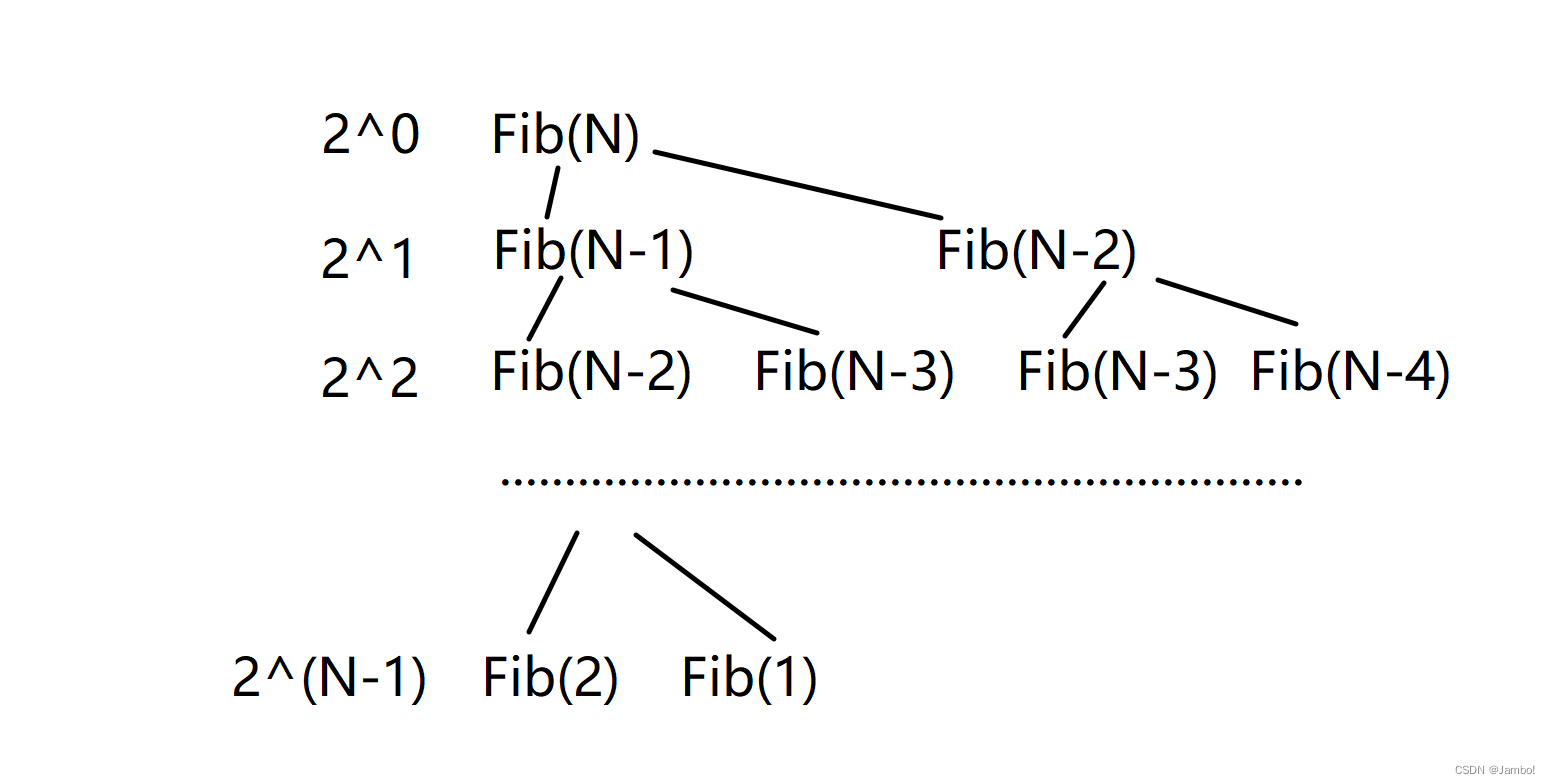
可以看出这个递归方法的时间复杂度是O(2^n)

可能这是没觉得时间复杂度是O(2^n)是多大的事，所以接下来我们计算一下传不同参数，这个递归算法的运行时间：

#include 
#include long long Fib(int n)
{if (n <= 2){return 1;}else{return Fib(n - 1) + Fib(n - 2);}
}
int main()
{int begin1 = clock();Fib(10);int end1 = clock();int begin2 = clock();Fib(20);int end2 = clock();int begin3 = clock();Fib(30);int end3 = clock();int begin4 = clock();Fib(40);int end4 = clock();int begin5 = clock();Fib(50);int end5 = clock();printf("end1:%d\n", end1 - begin1);printf("end2:%d\n", end2 - begin2);printf("end3:%d\n", end2 - begin3);printf("end4:%d\n", end4 - begin4);printf("end5:%d\n", end5 - begin5);return 0;
}

下面我们可以看到：
从参数从10~40的运行时间还算快，然而将50传入函数中，可以看到，会运行一段时间

所以使用递归方法求斐波那契数列在理论上可行，但是在实际中是不可取的一个方法

另外，我们在这也看一下2^N的“威力”

• N==10，2^N = 1024
• N==20，2^N = 100万
• N==30，2^N = 10亿
• N==40，2^N = 1万亿
• N==50，2^N = 很大很大的数

所以我们不能使用递归算法，接下来我们写一个迭代方法

迭代写法(效率高)

int feibonahi2(int n)
{if (n == 1 || n == 2){return 1;}int a = 1;int b = 1;int c = 1;while (n > 2){c = a + b;a = b;b = c;n--;}return c;
}

这个算法的时间复杂度是O(N),上面的递归写法要好的太多太多