本文属于「征服LeetCode」系列文章之一，这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁，本系列将至少持续到刷完所有无锁题之日为止；由于LeetCode还在不断地创建新题，本系列的终止日期可能是永远。在这一系列刷题文章中，我不仅会讲解多种解题思路及其优化，还会用多种编程语言实现题解，涉及到通用解法时更将归纳总结出相应的算法模板。

为了方便在PC上运行调试、分享代码文件，我还建立了相关的仓库。在这一仓库中，你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等，还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解，还可以一同分享给他人。

由于本系列文章的内容随时可能发生更新变动，欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。

You are the operator of a Centennial Wheel that has four gondolas, and each gondola has room for up to four people. You have the ability to rotate the gondolas counterclockwise, which costs you runningCost dollars.

You are given an array customers of length n where customers[i] is the number of new customers arriving just before the ith rotation (0-indexed). This means you must rotate the wheel i times before the customers[i] customers arrive. You cannot make customers wait if there is room in the gondola. Each customer pays boardingCost dollars when they board on the gondola closest to the ground and will exit once that gondola reaches the ground again.

You can stop the wheel at any time, including before serving all customers. If you decide to stop serving customers, all subsequent rotations are free in order to get all the customers down safely. Note that if there are currently more than four customers waiting at the wheel, only four will board the gondola, and the rest will wait for the next rotation.

Return the minimum number of rotations you need to perform to maximize your profit. If there is no scenario where the profit is positive, return -1.

Example 1:

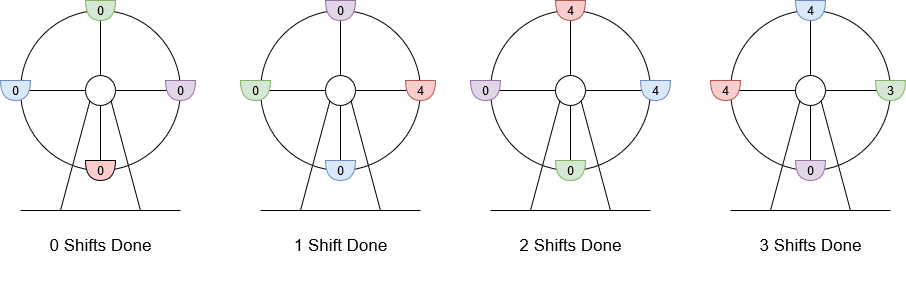
Input: customers = [8,3], boardingCost = 5, runningCost = 6
Output: 3
Explanation: The numbers written on the gondolas are the number of people currently there.
1. 8 customers arrive, 4 board and 4 wait for the next gondola, the wheel rotates. Current profit is 4 * $5 - 1 * $6 = $14.
2. 3 customers arrive, the 4 waiting board the wheel and the other 3 wait, the wheel rotates. Current profit is 8 * $5 - 2 * $6 = $28.
3. The final 3 customers board the gondola, the wheel rotates. Current profit is 11 * $5 - 3 * $6 = $37.
The highest profit was $37 after rotating the wheel 3 times.

Example 2:

Input: customers = [10,9,6], boardingCost = 6, runningCost = 4
Output: 7
Explanation:
1. 10 customers arrive, 4 board and 6 wait for the next gondola, the wheel rotates. Current profit is 4 * $6 - 1 * $4 = $20.
2. 9 customers arrive, 4 board and 11 wait (2 originally waiting, 9 newly waiting), the wheel rotates. Current profit is 8 * $6 - 2 * $4 = $40.
3. The final 6 customers arrive, 4 board and 13 wait, the wheel rotates. Current profit is 12 * $6 - 3 * $4 = $60.
4. 4 board and 9 wait, the wheel rotates. Current profit is 16 * $6 - 4 * $4 = $80.
5. 4 board and 5 wait, the wheel rotates. Current profit is 20 * $6 - 5 * $4 = $100.
6. 4 board and 1 waits, the wheel rotates. Current profit is 24 * $6 - 6 * $4 = $120.
7. 1 boards, the wheel rotates. Current profit is 25 * $6 - 7 * $4 = $122.
The highest profit was $122 after rotating the wheel 7 times.

Example 3:

Input: customers = [3,4,0,5,1], boardingCost = 1, runningCost = 92
Output: -1
Explanation:
1. 3 customers arrive, 3 board and 0 wait, the wheel rotates. Current profit is 3 * $1 - 1 * $92 = -$89.
2. 4 customers arrive, 4 board and 0 wait, the wheel rotates. Current profit is 7 * $1 - 2 * $92 = -$177.
3. 0 customers arrive, 0 board and 0 wait, the wheel rotates. Current profit is 7 * $1 - 3 * $92 = -$269.
4. 5 customers arrive, 4 board and 1 waits, the wheel rotates. Current profit is 11 * $1 - 4 * $92 = -$357.
5. 1 customer arrives, 2 board and 0 wait, the wheel rotates. Current profit is 13 * $1 - 5 * $92 = -$447.
The profit was never positive, so return -1.

Constraints:

• n == customers.length
• 1 <= n <= 105
• 0 <= customers[i] <= 50
• 1 <= boardingCost, runningCost <= 100

题意：作为一个有4个座舱 gondolas（每个座舱可容纳四个人）的摩天轮 Centennial Wheel 的操作员，你能让摩天轮逆时针旋转，每次轮转都需 runningCost 运行成本。给出长度为 n 的数组 customers ，customers[i] 是在第 i 次轮转（从0开始）前到达的新游客数量，这意味着你必须在新游客到来前旋转摩天轮 i 次。或者说，customers[i] 个游客到达后，才旋转第 i + 1 次。

你不能在摩天轮座舱还有空间时让游客等待，即能上多少游客就要上多少游客。每个游客登上座舱时给你带来 boardingCost 收入。一旦座舱到达地面，游客就离开。如果有超过四个游客在等待，则只有四个游客能登上座舱，其他游客等待下次轮转。

你可以在任何时间停止摩天轮，包括在服务所有游客之前 before serving all customers，即不开了、我们不提供服务。 如果你决定停止服务游客，为了使所有游客安全下地，所有后续轮转都是免费的。**返回能最大化利润的最小轮转次数。如果没有正利润方案，则返回 -1 。

解法 模拟+数组

轮转摩天轮分成两个阶段。第一阶段是前 nnn 次轮转，每次轮转之前都可能有新游客到达。如果在第一阶段结束之后，还有剩余的游客在等摩天轮，则进入第二阶段，将剩余的游客轮转完毕。无论在第一阶段还是第二阶段，我们都可以随时停止摩天轮，只要我们已经获得了最大利润，就可以立刻停下来、不继续轮转。而且，停止后如果还有游客在摩天轮上，则后续所有轮转都是无成本的、也没有利润（不让新游客登上摩天轮）。

对于第一阶段的每次轮转，需要首先计算该次轮转时正在等摩天轮的游客的数量，然后计算该次轮转的利润以及总利润，同时维护最大利润与最大利润的最小轮转次数。具体而言，第 iii 次轮转的流程如下：

1. customers[i]\textit{customers}[i]customers[i] 是在第 iii 次轮转之前到达的新游客的数量（iii 从 000 开始），使用 customers[i]\textit{customers}[i]customers[i] 的值，更新正在等摩天轮的游客的数量；
2. 计算登上座舱的游客的数量 curCustomerscurCustomerscurCustomers ，为「正在等摩天轮的游客的数量」和「座舱可以容纳的游客的数量」的最小值；
3. 从正在等摩天轮的游客的数量中减去登上座舱的游客的数量；
4. 计算该次轮转的利润，并计算到该次轮转的总利润，假设每位游客需要支付的费用是 boardingCostboardingCostboardingCost ，一次轮转有 curCustomerscurCustomerscurCustomers 位游客登上座舱，每次轮转的运行成本是 runningCostrunningCostrunningCost ，则摩天轮当前一次轮转的利润是 curCustomers×boardingCost−runningCostcurCustomers \times boardingCost - runningCostcurCustomers×boardingCost−runningCost ；
5. 如果总利润大于最大利润，则更新最大利润与最大利润的最小轮转次数（为 i+1i + 1i+1 ，因为 customers[i]customers[i]customers[i] 是在第 iii 次轮转前到来的新游客数目，现在完成了第 iii 次轮转，实际上进行了 i+1i + 1i+1 次轮转）。

第一阶段结束后，如果没有剩余的游客在等摩天轮，则直接返回最大利润的最小轮转次数。如果还有剩余的游客在等摩天轮，只有当剩余的游客带来的利润为正时，才需要考虑第二阶段，可能获得更多的利润。

由于每位游客需要支付的费用是正数，因此当座舱满舱时（即座舱上有 444 位游客，达到最大容纳数量），可以达到一次轮转的最大利润。

• 如果一次轮转的最大利润不为正，则第二阶段的利润一定不为正，因此直接返回第一阶段的最大利润的最小轮转次数。
• 如果一次轮转的最大利润为正，则每次座舱满舱的轮转的利润都为正，因此计算全部满舱轮转之后的总利润，如果大于最大利润，则更新最大利润与最大利润的最小轮转次数。最后可能剩下少于 444 位游客，需要进行最后一次非满舱的轮转，在最后一次轮转之后计算总利润，如果总利润大于最大利润，则更新最大利润与最大利润的最小轮转次数。

代码如下所示：

• 时间复杂度：O(n)O(n)O(n)
• 空间复杂度：O(1)O(1)O(1)

class Solution {
public:int minOperationsMaxProfit(vector& customers, int boardingCost, int runningCost) {int profit = 0, maxProfit = 0, maxTimes = -1, remains = 0; for (int i = 0, n = customers.size(); i < n || remains; ++i) {if (i < n) remains += customers[i];int t = (remains > 4) ? 4 : remains;remains -= t;profit += t * boardingCost - runningCost;if (profit > maxProfit) {maxProfit = profit;maxTimes = i + 1; // 注意是i+1}}return maxTimes;}
};